形式言語を簡便に表記する方法に正規表現があります。正規表現は、検索エンジンや grep などのコマンド、プログラミング言語などでサポートされているので使ったことがあるかもしれません。この章では正規表現を紹介したあと、正規言語との関係性をみていきます。
単一の文字からなる集合、空文字 \(\varepsilon\)、空集合 \(\emptyset\) に正規演算を任意回数施した式表現を正規表現という。
たとえば \((((\{0\} \circ \{1\}) \cup \{0\})*) \circ (\{0\} \circ \{0\} \circ \{0\})\) は正規表現です。単一の文字からなる集合の中括弧は煩雑なので通常省略されます。また、\(R_1 \circ R_2\) は \(\circ\) を省略して \(R_1 R_2\) と表記されることもあります。これは、かけ算の記号が省略されるようなものです。結合の強さは \(*\) が最も強く、次いで \(\circ, \cup\) となり、括弧は適宜省略される場合があります。これらのルールを適用すると、上述の集合は \((01 \cup 0)*000\) と表せます。
例をいくつか見てみましょう。なぜそのような言語を表すことになるのか考えてみてください。\(\Sigma = \{0, 1\}\) とします。
- \(0*10*\) は「1を一つ以上含む文字列全体」を表します。
- \((0 \cup 1)* 000 (0 \cup 1)*\) は「0を三つ連続で含む文字列全体」を表します。
- \(1 (0 \cup 1)*\) は「1から始まる文字列全体」を表します。
正規表現で正規演算以外の演算子を見たことがある方もいるかもしれません。
例えば + は 1 回以上の繰り返しを表します。この記法を使えば、「1から始まる文字列全体」は \(1+0*\) と表せます。
なぜこの + 記号が上記の定義に入っていないかというと、正規表現 \(R\) について \(R+\) は \(R R*\) と等価だからです。つまり、\(R+\) は \(R R*\) と書く手間を減らすだけの単なる略記方だと見ることができ、+ 記号を定義に加えると定義が冗長になってしまいます。
このような例は他にもあります。例えば、\(\Sigma\) がアスキー文字全体のとき、[0-9] という表現は数字全体を表します。これも \((0 \cup 1 \cup 2 \cup 3 \cup 4 \cup 5 \cup 6 \cup 7 \cup 8 \cup 9)\) の略記法だと見ることができます。また、\(.\) を使って一文字集合全体を表すこともあります。例えば \(\Sigma = \{0, 1\}\) のとき \(.\) は \(0 \cup 1\) と等価です。
これらの表記は簡便なのでよく使われますが、これらの表記を使ったときも常に三つの正規演算で書き直すことができることを心に留めておいてください。このように、冗長ではあるが分かりやすさのために使われる略記法のことを糖衣構文といいます。
これらの糖衣構文を使うとさらに複雑な言語が簡単に表せます。
- 上記で見た「0を三つ連続で含む文字列全体」は\(.*000.*\) で表せます。
- \((…)*\) は「長さが三の倍数の文字列全体」を表します。それぞれの \(.\) は別の文字を表していても良いことに注意してください。例えば 000 だけでなく 010 も \(…\) の要素です。
- \(0.*0 \cup 1.1 \cup 0 \cup 1\) は「最初と最後の文字が同じ文字列全体」を表します。
\(\Sigma\) としてアスキー文字全体を取ると、以下のような言語の表現もできます
- \([0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]\) は「郵便番号を表す文字列」を表します。
- \(Takahashi.*\) は「Takahashiからはじまる文字列全体」を表します。
同じ言語を表す正規表現も一通りではないことに注意してください。
正規表現は任意の正規言語を、そして正規言語のみを表現できます。これを数学的に示します。
正規表現で表現される言語は正規言語である。
これは前章の結果を使えば明らかです。
文字一文字からなる言語、空文字列のみからなる言語、空集合は正規言語である。前章の議論より、これらに正規演算を施したものは正規言語である。よって、正規表現で表現される言語は正規言語である。
任意の正規言語は正規表現で表現できる。
こちらは難しいです。正規言語を任意に取ったとき、その言語を認識するオートマトンを用意し、このオートマトンを正規表現で表します。いきなりオートマトン全体を表す正規表現を構築するのは難しいので、一部分を表す正規表現を構築し、それを組み合わせて徐々に大きな部分を表現していきます。
正規言語 \(A\) を任意にとる。\(A\) が正規表現で表されることを示す。\(A\) を認識する決定性有限オートマトンを \(M = (Q, \Sigma, \delta, q_0, F)\) とする。\(Q\) の要素数を \(n\) とし、\(Q\) の要素を \(1, 2, \cdots, n\) と番号づける。以下、状態と番号を同一視して呼ぶ。
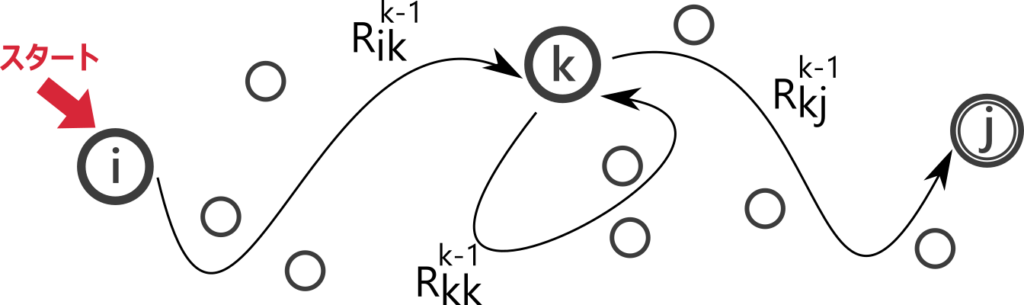
\(i, j \in \{1, 2, \cdots, n\}\) および \(k \in \{0, 1, 2, \cdots, n\}\)について、\(R_{ij}^k\) を「\(i, j\) 以外で番号が \(k\) より大きい状態を \(M\) から取り除き、\(i\) を開始状態、\(j\) のみを受理状態としたオートマトン \(M_{ij}^k\) が認識する言語」を表す正規表現とする。これが全て正規表現で表現できれば、\(M\) が受理する言語は \(\bigcup_{q \in F} R_{q_0 q}^n\) という正規表現で表せる。\(R_{ij}^k\) を \(k\) が小さい順に再帰的に求める。
1. \(k = 0\) のとき、状態は \(i, j\) しかない。
a) \(i \neq j\) のとき、\(R_{ij}^0 = \bigcup_{c \in \Sigma, \delta(i, c) = j} c\) と表せる。これは正規表現。
b) \(i = j\) のとき、\(R_{ij}^0 = (\bigcup_{c \in \Sigma, \delta(i, c) = i} c)*\) と表せる。これは正規表現。
2. \(k = l\) までの全ての \(R_{ij}^k\) が正規表現で表せたとして \(k = l+1\) のとき。状態 \(k\) を一度も通らずに受理される文字列集合は \(R_{ij}^{k-1}\) で表される。状態 \(k\) をちょうど一回通り受理される文字列は、途中で一度も \(k\) を通らず \(i\) から \(k\) に行く部分と、途中で一度も \(k\) を通らず \(k\) から \(j\) に行く部分とに分けられるので \(R_{ik}^{k-1} R_{kj}^{k-1}\) で表される。状態 \(k\) をちょうど二回通り受理される文字列は、途中で一度も \(k\) を通らず \(i\) から \(k\) に行く部分と、途中で一度も \(k\) を通らず \(k\) から \(k\) に行く部分と、途中で一度も \(k\) を通らず \(k\) から \(j\) に行く部分とに分けられるので \(R_{ik}^{k-1} R_{kk}^{k-1} R_{kj}^{k-1}\) で表される。同様に、状態 \(k\) をちょうど三回通り受理される文字列は \(R_{ik}^{k-1} R_{kk}^{k-1} R_{kk}^{k-1} R_{kj}^{k-1}\) と表され、四回通る文字列は\(R_{ik}^{k-1} R_{kk}^{k-1} R_{kk}^{k-1} R_{kk}^{k-1} R_{kj}^{k-1}\) と表せる。これを繰り返すと、途中で一回以上 \(k\) 通る文字列は \(R_{ik}^{k-1} (R_{kk}^{k-1}*) R_{kj}^{k-1}\) と表されることがわかる。これらを全てまとめると、\(R_{ij}^k = R_{ij}^{k-1} \cup R_{ik}^{k-1} (R_{kk}^{k-1}*) R_{kj}^{k-1}\) と表せる。これは正規表現。
グラフアルゴリズムを既に学んだ人はこの証明がフロイドワーシャルのアルゴリズムに似ていることに気づいた方もいるかもしれません。
- タネとなる単純な言語に正規演算を繰り返し適用してできる式を正規表現という
- 正規表現により表現される言語は正規言語である
- 逆に、全ての正規言語を正規表現により表すことができる
