ポンピング補題: 形式言語理論入門 10

背理法により示す。\(A\) が正規言語と仮定する。ポンピング補題より、ポンピング長 \(p\) が存在する。\(w = 0^p 1^p\) と取ると、\(w \in A\) および \(|w| \ge p\) より、ポンピング補題の条件を満たすように \(w = xyz\) と分解できる。

1. \(y\) が \(0\) のみを含むとすると、\(xy^2z\) は 1 の個数より 0 の個数が多くなるので \(xy^2z \not \in A\) となりポンピング補題の条件を満たさない。
2. \(y\) が \(1\) のみを含むとすると、\(xy^2z\) は 0 の個数より 1 の個数が多くなるので \(xy^2z \not \in A\) となりポンピング補題の条件を満たさない。
3. \(y\) が \(0\) と \(1\) を含むとすると、\(xy^2z\) は 0 の前に 1 が来ることになるので \(xy^2z \not \in A\) となりポンピング補題の条件を満たさない。

よって矛盾。\(A\) は正規言語でない。

背理法により示す。\(A\) が正規言語と仮定する。ポンピング補題より、ポンピング長 \(p\) が存在する。\(w = 0^p 1 0^p\) と取ると、\(w \in A\) および \(|w| \ge p\) より、ポンピング補題の条件を満たすように \(w = xyz\) と分解できる。

ポンピング補題の三つ目の条件より、\(y\) は \(0\) のみを含む。

\(xy^2z\) は \(s > t\) により \(0^s10^t\) と表されるので回文ではない。\(xy^2z \not \in A\) となりポンピング補題の条件を満たさない。

よって矛盾。\(A\) は正規言語でない。

\(A\) を正規言語とすると、\(A\) を認識する決定性有限オートマトン \(M = (Q, \Sigma, \delta, q_0, F)\) が存在する。

\(p = |Q|\) とおく。

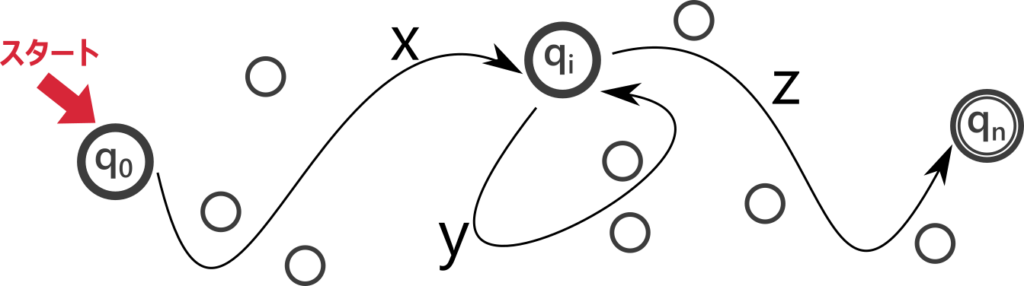
任意に長さが \(p\) 以上の文字列 \(w = c_1 c_2 \cdots c_n \in A\) をとる。\(w\) を \(M\) に入力したときの状態列を \(q_0 q_1 \cdots q_n\) とすると、\(n \ge p\) と鳩の巣原理より、\(q_i = q_j, (0 \le i < j \le p)\) となる \(i, j\) が存在する。\(x = c_1 c_2 \cdots c_{i}, y = c_{i+1} c_{i+2} \cdots, c_{j}, z = c_{j+1} c_{j+2} \cdots c_n\) とおく。\(i = 0\) のとき \(x\) が空文字であることに注意。こうすると \(w = x y z\) となり、

1. \(|y| \ge 1\)
2. \(|xy| \le p\)

となる。また、任意の \(k \ge 0\) について \(w’ = x y^k z\) とおくと、\(w’\) を \(M\) に入力したとき、状態列は \(q_0, q_1, \cdots, q_i, q_{i+1}, \cdots, q_{j}, q_{i+1}, q_{i+2}, \cdots, q_{j}, q_{i+1} q_{i+2}, \cdots, \cdots, q_{j}, q_{j+1}, \cdots, q_n\) というように、\(q_i, q_{i+1}, \cdots, q_j\) の間でループすることを除けば \(w\) と同じように遷移し最終的に受理状態 \(q_n\) にたどり着く。よって

3. \(w’ = x y^k z \in A\)。

以上より、ポンピング補題が成立する。