この章では決定性有限オートマトンを数学的に定義します。議論が抽象的になりますが、前章での図を使った議論を頭に入れて読めば分かりやすいと思います。
決定性有限オートマトンは五つの要素を決めれば定まります。一つ目は文字の集合は何か、二つ目は状態の集合、三つ目は遷移の方法、四つ目は開始状態はどの状態か、五つ目はどの状態が受理状態か、です。一つずつ要素を見ていきましょう。
言語に含まれることが許される文字の集合を \(\Sigma\) と表します。\(\Sigma\) のことをアルファベットと呼ぶこともありますが、abcdefg…, というあのアルファベット（ラテン文字）とは無関係の用語です。前章での例では \(\Sigma=\{0, 1\}\) でした。一般には一章目の例のように \(\Sigma\) としてひらがなとカタカナと漢字を全部合わせた集合でも良いです。文字の種類が多いと煩雑になるので今後は基本的には \(\Sigma=\{0, 1\}\) とします。
状態の集合を \(Q\) と表します。決定性有限オートマトンではその名の示す通り \(Q\) は有限集合でなければなりません。\(Q\) の要素自体は意味はなく、要素数だけが本質的です。例えば \(Q = \{A, B, C\}\) でも \(Q = \{いちご, りんご, バナナ\}\) でも本質的な意味は変わりません。この講義では基本的に大文字のアルファベットを状態を表す記号として使います。
各状態について、各文字を読み込んだときにどの状態に移るかが決まってなければなりません。数学的にはこれを、状態と文字を受け取ったときに状態を返す関数 \(\delta\colon Q \times \Sigma \to Q\) で表します。この関数を遷移関数といいます。例えば、状態 \(A \in Q\) にあるとき文字 \(1 \in \Sigma\) を受け取って状態 \(B \in Q\) に遷移するのであれば \(\delta(A, 1) = B\) のように表します。
まだ何も文字を読み込んでいない時点での状態を開始状態といい \(q_0 \in Q\) で表します。オートマトンの図でいうところの「スタート」と書かれた状態に相当します。開始状態は状態集合のうちのどれかで、二つ以上はなく、ちょうど一つだけあります。
全部の文字を読み取り終わった時点で、その状態にいたら受理する状態を受理状態といい、 \(F \subseteq Q\) で表します。オートマトンの図でいうところの二重丸の状態に相当します。受理状態は存在しないこともあれば、二つ以上存在することもあります。存在しない場合は \(F\) は空集合となります。
決定性有限オートマトンとは五つ組 \((\Sigma, Q, \delta, q_0, F)\) である。ただし、\(\Sigma\) は文字を表す有限集合、\(Q\) は状態を表す有限集合、\(\delta\colon Q \times \Sigma \to Q\) は遷移関数、\(q_0 \in Q\) は初期状態、\(F \subseteq Q\) は受理状態である。
数学的には、丸と矢印からなる図ではなく、この五つ組こそが決定性有限オートマトンになります。丸と矢印からなる図は決定性有限オートマトンを分かりやすく図示したものに過ぎません。ちょうど \(f(x) = x^2\) こそが関数であって、放物線を描くグラフは関数そのものではなく図示にすぎないことと同じです。
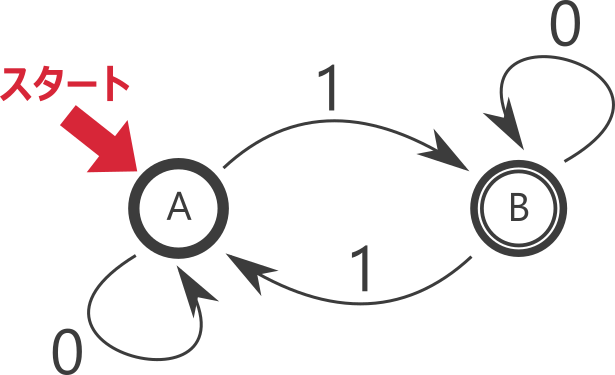
前章で見た、上記の「1を奇数個含む文字列」に相当するオートマトンは
\(\Sigma = \{0, 1\}\), \(Q = \{A, B\}\), \(\delta(A, 0) = A\), \(\delta(A, 1) = B\), \(\delta(B, 0) = B\), \(\delta(B, 1) = A\), \(q_0 = A\), \(F = \{B\}\) で表されます。
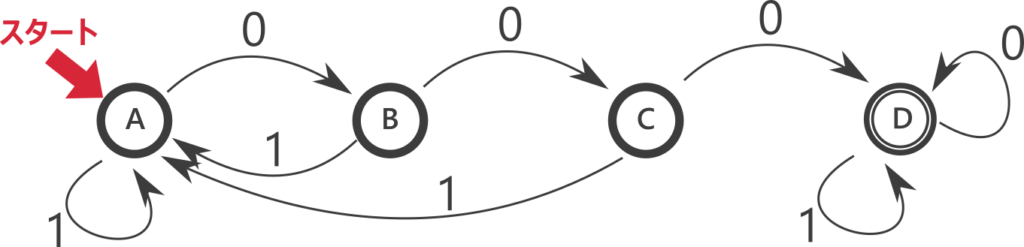
上記の「0を三つ連続で含む文字列」に相当するオートマトンは
\(\Sigma = \{0, 1\}\), \(Q = \{A, B, D, D\}\), \(\delta(A, 0) = B\), \(\delta(A, 1) = A\), \(\delta(B, 0) = C\), \(\delta(B, 1) = A\), \(\delta(C, 0) = D\), \(\delta(C, 1) = A\), \(\delta(D, 0) = D\), \(\delta(D, 1) =D\), \(q_0 = A\), \(F = \{D\}\) で表されます。
- オートマトンとは、数学的には、文字集合、状態集合、遷移関数、開始状態、受理状態の五つの組で定義される。
