この章では、前章で作った全加算器を組み合わせ、複数桁の足し算ができる計算機を完成させます。
複数桁の足し算を行う回路を考えます。とりあえず二進数 4 桁の足し算を考えましょう。より多くの桁には簡単に拡張できます。
入力の各数が 4 桁なので、入力端子は 8 個です。入力された数を \(A, B\) と表し、対応する端子を \(A_1, A_2, A_3, A_4\) および \(B_1, B_2, B_3, B_4\) と表します。出力は繰り上がりまで考慮すると 5 桁になるかもしれないので、出力端子は 5 個とします。出力する数を \(C\) と表し、対応する端子を \(C_1, C_2, C_3, C_4, C_5\) と表します。
例えば、\(A = 5, B = 7\) の場合を考えましょう。二進数で表すと \(5\) は \(0101\)、\(7\) は \(0111\) なので、論理回路には \(A_1 = 1, A_2 = 0, A_3 = 1, A_4 = 0, B_1 = 1, B_2 = 1, B_3 = 1, B_4 = 1\) を入力することになります。出力は \(C = A + B = 5 + 7 = 12\) で、\(12\) は二進数で表すと \(01100\) なので、\(C_1 = 0, C_2 = 0, C_3 = 1, C_4 = 1, C_5 = 0\) が出力されるようにします。
入力端子が \(8\) 個もあると真理値表は \(256\) 行にもなるのでとても書いていられません。パターンは膨大ですが、これまで作ってきた半加算器や全加算器を組み合わせると簡単に実装することができます。
4 桁の足し算の 1 桁目の答え \(C_1\) は単に入力の 1 桁目 \(A_1\) と \(B_1\) を足し合わせるだけです。これは半加算器で実現できます。
2 桁目の出力 \(C_2\) は、2 桁目からの繰り上がりと、各入力の 2 桁目 \(A_2\) と \(B_2\) を足し合わせることで求められます。これは全加算器で実現できます。
3 桁目、4 桁目の出力も同様に前の桁からの繰り上がりと、各入力の対応する桁を足し合わせると求められるので、全加算器で実現できます。
5 桁目の出力は 4 桁目からの繰り上がりそのままです。
よって、4 桁の足し算を行う回路は以下のように表せます。
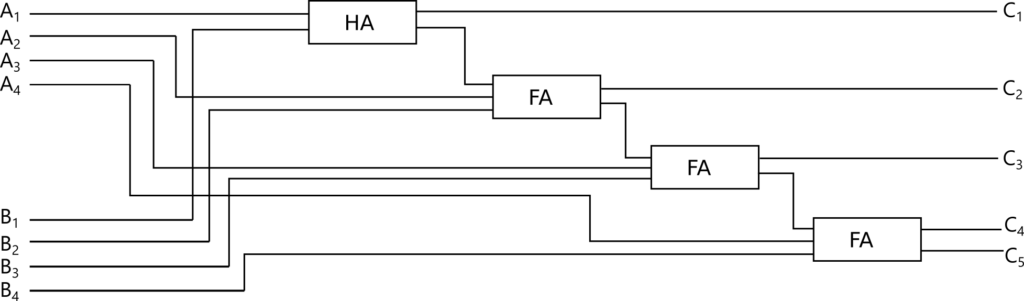
8 桁やもっと大きな桁の場合も連結する全加算器の数を増やすだけで実現できます。
今後、この加算器を使い回すために抽象化しておきましょう。\(n\) 桁の加算器 (adder) は Add\(n\) と書いた四角形で表すことにします。例えば 4 桁であれば Add4 と表します。
また、桁数が多くなってくると配線をたくさん書くのが面倒です。同じ機能をになっているひとまとまりの配線は、一本一本書くのではなく、太い線一本で表すことにしましょう。例えば、以下のように略記します。

太い線というパーツがあるのではなく、あくまで複数の配線の略記法であることに注意してください。
太い線が何本の線のまとまりであるかを表しているかは文脈次第です。Add4 に入っていたら 4 本なんだというように推測してください。また、どのように太い線をまとめるかも文脈依存です。例えば Add4 に入力される 2 数全部まとめて 8 つの配線を太線で表すことも理論上はできますが、通常はそのようなことはせず、4 桁ずつの太い線 2 本で表します。慣れないうちはややこしいですが慣れると便利な記法なので慣れていきましょう。
複数桁の足し算を行う計算機を実装してみましょう。といっても、肝心の足し算を行うメインロジック部分は上で構築したので、あとは入力部分と出力部分を付け加えるだけです。
入力部分はスイッチで信号を与えられるようにしましょう。押すと電流が流れるスイッチを加算器の入力につなげます。
出力部分は第一章の冒頭で述べたように LED をつなげましょう。LED には電流が流れると光るとします。
これを合わせると以下の図のように計算機が完成します。
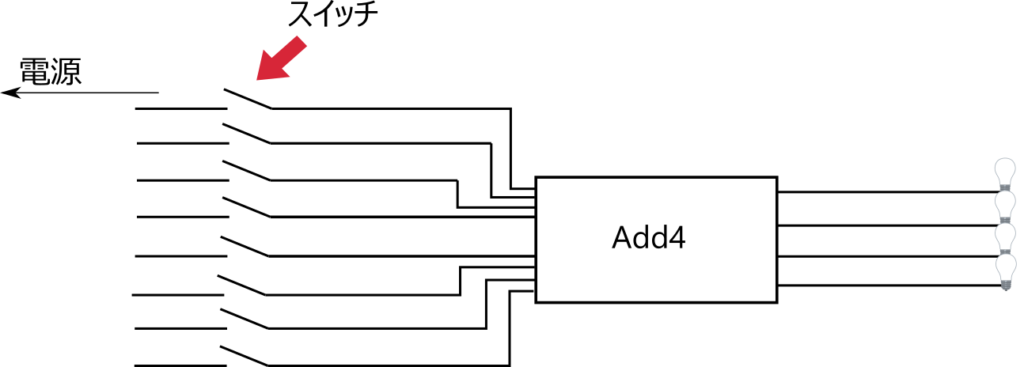
例えば、入力スイッチを 0101 と 0111 というパターンで押すと、LED は 1100 というパターンで光ります。
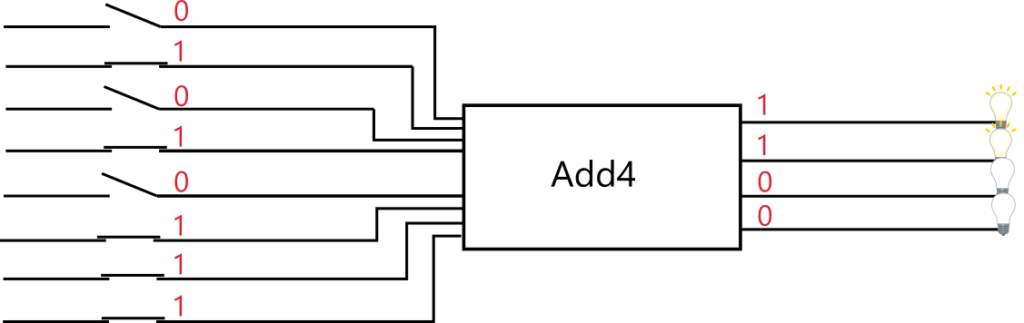
入力スイッチを 0100 と 1001 というパターンで押すと、LED は 1101 というパターンで光ります。
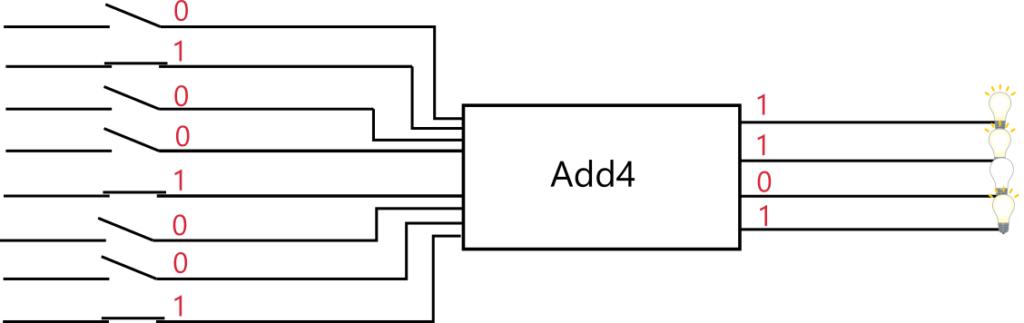
十進数ではなく二進数で入出力する点が違いますが、電卓のような機能を持った計算機が実現できました。
この計算機は足し算ができるだけで引き算やかけ算はできませんが、加算器と同じような要領で減算器や乗算器を設計すれば、引き算を行う計算機や、かけ算を行う計算機も実現できます。
しかし、電卓は一つの回路でいろんな計算ができるのに対し、このやり方では一つの回路で一つの機能しか持てない点が違います。その課題を解決するセレクタというパーツを次章で学びます。
また、電卓は過去の計算を記憶して順々に足し合わせたりすることができる点も異なります。そのような記憶回路については次々章以降で学んでいきます。
- 全加算器をつなぎ合わせることで複数桁の足し算を実現できる
- 加算器の入力にスイッチ、出力に LED をつなげると簡単な計算機が実現できる


