この章では最も簡単な計算機である半加算器を実装します。半加算器は二進数 1 桁の足し算を行う回路です。
半加算器は 2 つの入力端子 A, B をもち、2 つの出力端子 S, C をもつ、二進数 1 桁の足し算を表す回路です。直感的には二進数の足し算 A + B を表しています。S が一桁目の値、C が繰り上がりです。

入力が A = 0, B = 0 のときは出力が S = 0, C = 0 となり、入力が A = 0, B = 1 のときは出力は S = 1, C = 0、入力が A = 1, B = 0 のときは出力は S = 1, C = 0、入力が A = 1, B = 1 のときは出力は S = 0, C = 1 となります。
つまり、半加算器の入力値と出力値の対応は以下のようになります。
| A | B | S | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
このように、論理回路の入力値と出力値の組み合わせを列挙した表を真理値表とよびます。
この真理値表を満たすような回路を AND, OR, NOT 素子を組み合わせて実現します。
まず、定義から明らかなように C は A と B が両方 1 のときかつそのときのみ 1 をとります。これはまさに AND 素子の定義ですね。なので、C は AND 素子 1 つで実装できます。
S は A OR B に近いですが、A = 1, B = 1 のとき、つまり A AND B = 1 のときは例外的に S = 0 となります。これは S = (A OR B) AND NOT (A AND B) と書き表せることを意味します。このような式で書き表すと AND, OR, NOT 素子の組み合わせで実装できたようなものです。
以下の回路が半加算器を表します。
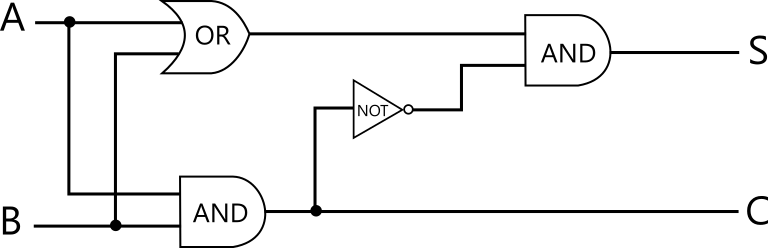
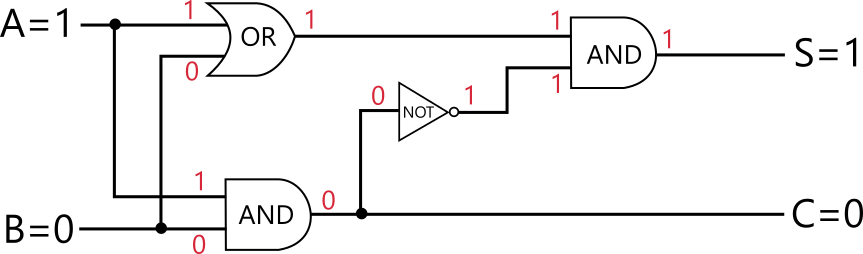
実際に動作を確かめてみましょう。例えば入力が A = 1, B = 0 のとき、各地点での値(電流が流れているかいないか)は以下のようになります。AND の両方の入力が 1 ならば出力部分は 0 というように各論理素子の前後で整合性がとれていることを確認してください。出力部分に着目すると、S = 1, C = 0 となり、正しく半加算器の要件が満たされていることが分かります。
例えば入力が A = 1, B = 1 のとき、以下のようになり、やはり正しく半加算器の要件が満たされていることが分かります。
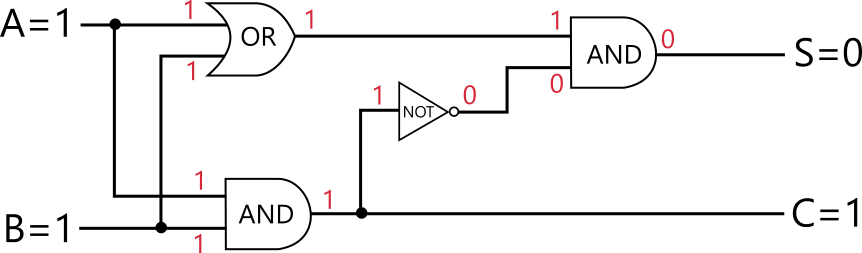
他の入力の場合も同様に、要件が満たされていることを確認することができます。
半加算器を AND, OR, NOT を使って実装する方法は一通りでないことに注意してください。例えば以下の回路も半加算器を表します。どう実装するかに関わりなく、上で述べた真理値表の通りに動作する回路であれば全て半加算器ということになります。
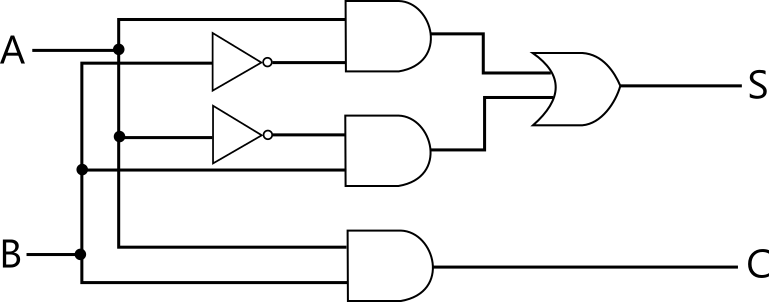
半加算器はいくつかの基本素子 AND, OR, NOT を使って実現されているわけですが、半加算器自体を一つの素子と見ることもできます。半加算器 (half adder) の回路を HA と書いた四角で表すことにします。以降はこれを基本素子と同じように扱いますが、これは AND, OR, NOT から構成される略記法だと考えてください。例えば以下の図の上のように書いたときは、実際は下のような回路図だということです。
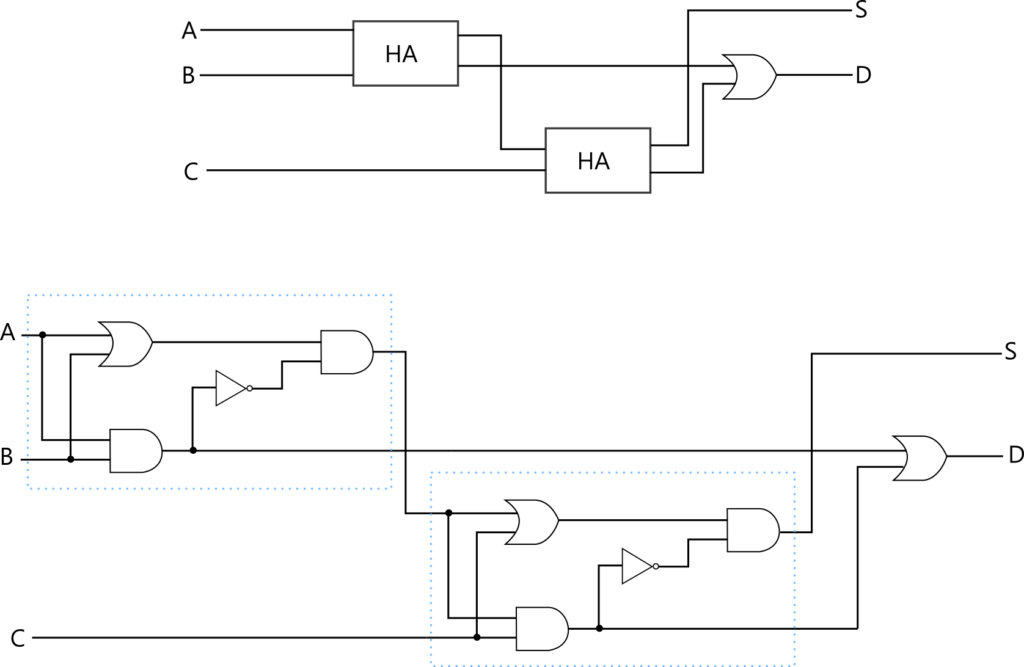
下の図はごちゃごちゃしていますが、上の図は一機能のパーツがまとまっておりすっきりしています。このように、より基本的なパーツからなるひとまとまりのグループを新たなパーツとみなすことを抽象化といいます。抽象化のおかげで、細かいごちゃごちゃした部分に気を取られずに、本質的な部分にのみ着目できるようになります。
- 二進数の 1 桁を足し算する回路を半加算器という
- 論理回路の要件は真理値表で表現できる
- 半加算器は AND, OR, NOT 素子の組み合わせで表現できる
- 半加算器を新たなパーツとみなす抽象化を行う
次の章では半加算器を複数桁の足し算に拡張するべく、全加算器というものを実装します。


