相互情報量と通信路容量: 情報理論入門 7

通信路を用いてどれだけ効率的に通信を行えるかは通信路容量という量を用いて表すことができます。まずは、通信路容量を定義するための基礎となる相互情報量について見ていきましょう。

エントロピー・相対エントロピー・相互情報量

エントロピー

離散値 $\mathcal{X} = \{x_1, x_2, \cdots, x_n\}$ をとる確率変数 $X$ を考えます。この確率変数のエントロピーは以下で定義されます。

定義: エントロピー

確率変数 $X$ のエントロピー $H(X) \in \mathbb{R}$ は以下で定義される。$$\begin{align*}H(X) &= – \sum_{x \in \mathcal{X}} P(X = x) \log_2 P(X = x) \\ &= \mathbb{E}_{X}[- \log_2 P(X)] \end{align*}$$ ただし、$0 \log_2 0 = 0$ と定義する。

直感的には、エントロピーは確率変数の乱雑さや不確かさを表しています。

例: 決定的な変数

$\mathcal{X} = \{0, 1\}$ とし、$P(X = 0) = 0, P(X = 1) = 1$ とする。つまり、$X$ は常に $1$ を取るとする。このとき、$$\begin{align*}H(X) &= – P(X = 0) \log_2 P(X = 0) – P(X = 1) \log_2 P(X = 1) \\ &= – 0 \log_2 0 – 1 \log_2 1 \\ &= 0\end{align*}$$

例: ランダムな変数

$\mathcal{X} = \{0, 1\}$ とし、$P(X = 0) = 0.5, P(X = 1) = 0.5$ とする。つまり、$X$ は $0, 1$ を同様に確からしい確率で取るとする。このとき、$$\begin{align*}H(X) &= – P(X = 0) \log_2 P(X = 0) – P(X = 1) \log_2 P(X = 1) \\ &= – 0.5 \log_2 0.5 – 0.5 \log_2 0.5 \\ &= – 0.5 \times (-1) – 0.5 \times (-1) \\ &= 1 \end{align*}$$

不確かさがない（確かである）決定的な変数ではエントロピーがゼロとなり、不確かさが大きいランダムな変数よりもエントロピーが小さいことからも、エントロピーが不確かさを表していることが分かります。

エントロピーは情報源符号化の項でも出てきました。そこでは、エントロピーは情報源を符号化するのに必要な平均符号長としての役割を果たしていました。決定的な情報源ほど、結果を伝えるのに必要な平均符号長は小さく、乱雑な情報源ほど、結果を伝えるのに必要な平均符号長は大きくなることからも、エントロピーが乱雑さを表していることが分かります。

同時エントロピー

離散値 $\mathcal{X} = \{x_1, x_2, \cdots, x_n\}$ をとる確率変数 $X$ と離散値 $\mathcal{Y} = \{y_1, y_2, \cdots, y_m\}$ をとる確率変数 $Y$ を考えます。同時エントロピーの定義は、エントロピーの定義を複数の確率変数の同時分布に拡張しただけの簡単なものです。

定義: 同時エントロピー

確率変数 $X, Y$ のエントロピー $H(X, Y) \in \mathbb{R}$ は以下で定義される。$$\begin{align*}H(X, Y) &= – \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} P(X = x, Y = y) \log_2 P(X = x, Y = y) \\ &= \mathbb{E}_{X, Y}[- \log_2 P(X, Y)] \end{align*}$$ ただし、$0 \log_2 0 = 0$ と定義する。

二つの確率変数を合わせた不確かさは、各確率変数の不確かさの和以下になります。

定理: 同時エントロピーはエントロピーの総和以下である

任意の確率変数 $X, Y$ について $H(X, Y) \le H(X) + H(Y)$が成り立つ

証明

$$\begin{align*}&H(X, Y) – H(X) – H(Y) \\&= \mathbb{E}_{X, Y}\left[- \log_2 P(X, Y)\right] – \mathbb{E}_{X}\left[- \log_2 P(X)\right] – \mathbb{E}_{Y}\left[- \log_2 P(Y)\right]\\ &\stackrel{(a)}{=}\mathbb{E}_{X, Y}\left[\log_2 P(X) + \log_2 P(Y) – \log_2 P(X, Y)\right] \\ &\stackrel{(b)}{=} \mathbb{E}_{X, Y}\left[\log_2 \frac{P(X) P(Y)}{P(X, Y)}\right] \\ &\stackrel{(c)}{\le} \log_2\mathbb{E}\left[\frac{P(X) P(Y)}{P(X \mid Y)}\right] \\ &= \log_2 \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} P(X = x, Y = y) \frac{P(X = x) P(Y = y)}{P(X = x, Y = y)} \\ &= \log_2 \sum_{y \in \mathcal{Y}} P(Y = y) \sum_{x \in \mathcal{X}} P(X = x) \\ &\stackrel{(d)}{=} \log_2 1 \\ &= 0 \end{align*}$$

よって $H(X \mid Y) \le H(X)$ が成り立つ。ただし、(a) では期待値の線形性を、(b) では対数の性質を、(c) では対数が凹であることとイェンゼンの不等式を、(d) では確率値の総和が $1$ であることを用いた。

等号が必ずしも成り立たないのは、$X$ と $Y$ は独立していない場合があるからです。極端な例では、$X = Y$ とすると、$H(X, X) = H(X)$ となるので $H(X) + H(X) = 2H(X)$ とは一致しません。一方、$X, Y$ が独立であれば、上記証明中の (b) のあとで $P(X, Y) = P(X) P(Y)$ となり、対数の中が $1$ となって左辺が $0$ になり、$H(X, Y) = H(X) + H(Y)$ と等号成立することが分かります。

相対エントロピー

相対エントロピーは、二つの確率変数があったとき、一方の確率変数で条件づけたときのエントロピーとして定義されます。離散値 $\mathcal{X} = \{x_1, x_2, \cdots, x_n\}$ をとる確率変数 $X$ と離散値 $\mathcal{Y} = \{y_1, y_2, \cdots, y_m\}$ をとる確率変数 $Y$ を考えます。$Y$ で条件づけた $X$ の相対エントロピーは以下で定義されます。

定義: 相対エントロピー

確率変数 $X, Y$ についての相対エントロピー $H(X \mid Y) \in \mathbb{R}$ は以下で定義される。$$\begin{align*}H(X \mid Y) &= – \sum_{y \in \mathcal{Y}} P(Y = y) \sum_{x \in \mathcal{X}} P(X = x \mid Y = y) \log_2 P(X = x \mid Y = y) \\ &= \mathbb{E}_{X, Y}[- \log_2 P(X \mid Y)] \end{align*}$$ ただし、$0 \log_2 0 = 0$ と定義する。

相対エントロピーはカルバック・ライブラーダイバージェンス（KL ダイバージェンス）とも呼ばれます。

一般に、$H(X \mid Y) \neq H(Y \mid X)$ であることに注意してください。

以下の定理に示されるように、確率変数で条件付けると不確かさは減少します。（正確にいうと、条件付けることでエントロピーが増加することはありません。条件づけてもエントロピーが変化しない場合は存在します。）

定理: 相対エントロピーはエントロピー以下である

任意の確率変数 $X, Y$ について $H(X \mid Y) \le H(X)$が成り立つ

証明

$$\begin{align*}&H(X \mid Y) – H(X) \\ &= \mathbb{E}_{X, Y}\left[- \log_2 P(X \mid Y)\right] – \mathbb{E}_{X}\left[- \log_2 P(X)\right]\\ &\stackrel{(a)}{=}\mathbb{E}_{X, Y}\left[\log_2 P(X) – \log_2 P(X \mid Y)\right] \\ &\stackrel{(b)}{=} \mathbb{E}_{X, Y}\left[\log_2 \frac{P(X)}{P(X \mid Y)}\right] \\ &\stackrel{(c)}{\le} \log_2\mathbb{E}\left[\frac{P(X)}{P(X \mid Y)}\right] \\ &= \log_2 \sum_{y \in \mathcal{Y}} P(Y = y) \sum_{x \in \mathcal{X}} P(X = x \mid Y = y) \frac{P(X = x)}{P(X = x \mid Y = y)} \\ &= \log_2 \sum_{y \in \mathcal{Y}} P(Y = y) \sum_{x \in \mathcal{X}} P(X = x) \\ &\stackrel{(d)}{=} \log_2 1 \\ &= 0 \end{align*}$$

例: 自分自身で条件付け

任意の確率変数 $X$ に対して $$\begin{align*}H(X \mid X) &= – \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{X}} P(X = x, X = y) \log_2 P(X = x \mid X = y) \\ &\stackrel{(a)}{=} – \sum_{x \in \mathcal{X}} P(X = x, X = x) \log_2 P(X = x \mid X = x) \\ &\stackrel{(b)}{=} – \sum_{x \in \mathcal{X}} P(X = x, X = x) \log_2 1 \\ &= 0\end{align*}$$

ただし、(a) では $x \neq y$ のとき $P(X = x, X = y) = 0$ を、(b) では $P(X = x \mid X = x) = 1$ を用いた。

自分の情報が分かっているときには、残っている不確かさはゼロとなるのは直感に適合します。

相互情報量

二つの確率変数の相互情報量は、一方の確率変数の値を知ることでもう一方の変数について得られる情報量を表します。これは、一方の変数で条件付けることで減少するエントロピー（不確かさ）によって定義されます。

定義: 相互情報量

確率変数 $X, Y$ についての相互情報量 $I(X; Y) \in \mathbb{R}$ は以下で定義される。

$$I(X; Y) = H(X) – H(X \mid Y)$$

$H(X) \ge H(X \mid Y)$ より、相互情報量は常に非負となります。

相対エントロピーは対称ではありませんが、相互情報量は対称であることが示せます。

定理: 相互情報量の対称性

任意の確率変数 $X, Y$ について、$I(X; Y) = I(Y; X)$ が成り立つ。

証明

$$\begin{align*}I(X; Y) &= H(X) – H(X \mid Y) \\ &= \mathbb{E}_{X}\left[-\log_2 P(X)\right] – \mathbb{E}_{X, Y}\left[-\log_2 P(X \mid Y)\right] \\ &\stackrel{(a)}{=} \mathbb{E}_{X, Y}\left[\log_2 P(X \mid Y) – \log_2 P(X)\right] \\ &\stackrel{(b)}{=} \mathbb{E}_{X, Y}\left[\log_2 \frac{P(X \mid Y)}{P(X)}\right]\\ &\stackrel{(c)}{=} \mathbb{E}_{X, Y}\left[\log_2 \frac{P(X, Y)}{P(X)P(Y)}\right] \\ &\stackrel{(d)}{=} \mathbb{E}_{X, Y}\left[\log_2 \frac{P(Y \mid X)}{P(Y)}\right] \\ &\stackrel{(e)}{=} \mathbb{E}_{X, Y}\left[\log_2 P(Y \mid X) – \log_2 P(Y)\right] \\ &\stackrel{(f)}{=} \mathbb{E}_{X}\left[-\log_2 P(Y)\right] – \mathbb{E}_{X, Y}\left[-\log_2 P(Y \mid X)\right] \\ &= H(Y) – H(Y \mid X) \\ &= I(Y; X)\end{align*}$$

ただし、(a) では期待値の線形性を、(b) では対数の性質を、(c) と (d) ではベイズの定理を、(e) では対数の性質を、(f) では期待値の線形性を用いた。

通信路容量

入力記号を $\mathcal{X}$、出力記号を $\mathcal{Y}$、通信路行列を $\mathbf{P} \in \mathbb{R}^{\mathcal{X} \times \mathcal{Y}}$ とする通信路を用いて通信することを考えます。すなわち、この通信路に記号 $x \in \mathcal{X}$ を入力すると、確率 $\mathbf{P}_{xy} = P(Y = y \mid X = x)$ で記号 $y \in \mathcal{Y}$ が出力されます。

通信路容量は、どのようにすればこの通信路を用いて最もよく通信ができるか、そしてそのときどれほどの情報を伝えられるかを定める非常に重要な概念です。

今考えている設定では、通信路が定める条件つき分布 $P(Y \mid X)$ は所与ですが、入力記号についての確率分布 $P(X)$ は使用者が決めることに注意してください。常に同じ記号を入力するような使い方をしても、相手には情報を伝えられません。全ての入力記号を等しい割合で使うことはより適切な候補ですが、通信路行列次第では最適ではないかもしれません。これを定量的に表すのが以下で定義される通信路容量です。

定義: 通信路容量

確率分布 $P(Y \mid X)$ により定まる通信路 $\mathcal{C}$ の通信路容量 $C(\mathcal{C})$ は $$C(\mathcal{C}) = \max_{p(X)} I(X; Y)$$ により定義される。ただし、$p(X)$ の最大化の対象は $\mathcal{X}$ の離散分布全体をとる。

最適化の観点からいえば、$C$ を求める問題は $|\mathcal{X}|$（入力記号の要素数）次元のベクトルが決定変数である最適化問題です。最適化の領域は $$\left\{\mathbf{x} \in \mathbb{R}_{\ge 0}^\mathcal{X} \mid \sum_{x \in \mathcal{X}} \mathbf{x}_x = 1\right\}$$（確率シンプレックス）となります。

また、目的関数は $$\begin{align*}I(X; Y) &= H(X) – H(X \mid Y) \\ &=- \sum_{x \in \mathcal{X}} p(X = x) \log_2 p(X = x) \\ &\qquad \qquad + \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} P(Y = y, X = x) \log_2 P(X = x \mid Y = y) \\ &\stackrel{(a)}{=} – \sum_{x \in \mathcal{X}} p(X = x) \log_2 p(X = x) \\ & \qquad \qquad + \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} \mathbf{P}_{xy} P(X = x) \log_2 \frac{\mathbf{P}_{xy} P(X = x)}{\sum_{x’ \in \mathcal{X}} \mathbf{P}_{x’y} P(X = x’)} \end{align*}$$

というように、$P(X = x)$ と $\mathbf{P}$ の式で書き表されます。ただし、(a) ではベイズの定理を用いました。

例: 壊れたボタン

入力記号を $\mathcal{X} = \{1, 2, 3\}$、出力記号を $\mathcal{Y} = \{1, 2, 3\}$ とし、通信路行列を $$\mathbf{P} = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0.5 & 0.5 & 0\end{pmatrix}$$ により定まる通信路を考える。これは、$1, 2$ は正しく相手に伝わるが、$3$ を入力したときには $1, 2$ がデタラメに出てくるような通信路である。$\mathbf{x}_x = P(X = x)$ とおくと、相互情報量は以下のように表せます。 $$\begin{align*} &\left(- \sum_{x \in \mathcal{X}} \mathbf{x}_x \log_2 \mathbf{x}_x\right) + \left(\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} \mathbf{P}_{xy} \mathbf{x}_x \log_2 \frac{\mathbf{P}_{xy} \mathbf{x}_x}{\sum_{x’ \in \mathcal{X}} \mathbf{P}_{x’y} \mathbf{x}_{x’}}\right) \\ &= \left(- \sum_{x \in \mathcal{X}} \mathbf{x}_x \log \mathbf{x}_x\right) \\ & \qquad + 1 \cdot \mathbf{x}_1 \log_2 \frac{\mathbf{x}_1}{\mathbf{x}_1 + 0.5 \mathbf{x}_3} +1 \cdot \mathbf{x}_1 \log_2 \frac{\mathbf{x}_2}{\mathbf{x}_2 + 0.5 \mathbf{x}_3} \\ & \qquad + 0.5 \cdot \mathbf{x}_3 \log_2 \frac{\mathbf{x}_3}{\mathbf{x}_1 + 0.5 \mathbf{x}_3} + 0.5 \cdot \mathbf{x}_3 \log_2 \frac{\mathbf{x}_3}{\mathbf{x}_2 + 0.5 \mathbf{x}_3}\end{align*}$$

この関数を $\mathbf{x}_1 \ge 0, \mathbf{x}_2 \ge 0, \mathbf{x}_3 \ge 0, \mathbf{x}_1 + \mathbf{x}_2 + \mathbf{x}_3 = 1$ の制約のもと最大化しましょう。$(\mathbf{x}_1, \mathbf{x}_2)$ における目的関数の値をプロットすると以下のようになります。（$\mathbf{x}_3$ は $\mathbf{x}_1, \mathbf{x}_2$ を決めると総和制約より一意に定まります。）

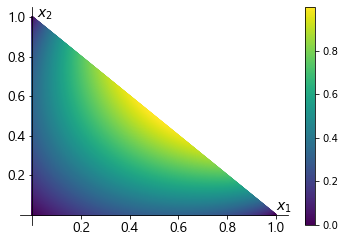
よって、この問題では $(\mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3) = (0.5, 0.5, 0.0)$ のとき最大となり、通信路容量は $1.0$ となります。図を頼らずともラグランジュの未定乗数法などで最適値を解析的に算出することができますが、煩雑なためここでは省略します。

$1, 2$ は正しく相手に伝わるが、$3$ を入力したときにはデタラメな値が出てくるので、$3$ は使わず、$1, 2$ を等割合で使うというのは直感にも合う結果かと思います。