通信路符号化の数学的な定式化: 情報理論入門 6

通信路符号化では、情報源符号化と異なり、信頼のできない通信路を用いて安定した通信を行うための符号化方法を考えます。送信者が送信した情報がその通りに受信者に届くとは限らず、何かしらのノイズが加わって届く場合、符号化に適度な冗長性を持たせることで、簡潔でありつつ誤りが避けられるようにすることを目指します。

問題設定

通信路符号化には送信者と受信者という二人の登場人物が登場します。電報のように送信者と受信者は異なる地点にいる異なる人間である場合もあれば、ファイル破損の冗長化の場合は過去の自分と未来の自分という時間的に離れた同一人物が対応する場合もあります。

通信路符号化では多くの場合、情報源というものは考えず、単に送信したいメッセージのパターン $\mathcal{M} = \{1, 2, \cdots, n\}$ が存在するとします。

送信者と受信者は通信路 $\mathcal{C} = (\mathcal{X}, \mathcal{Y}, P)$ を用いて通信を行います。ここで、$\mathcal{X}$ は入力記号、$\mathcal{Y}$ は出力記号、$P \in \mathbb{R}^{\mathcal{X} \times \mathcal{Y}}$ は通信路行列であり、この通信路に記号 $x \in \mathcal{X}$ を入力すると、確率 $P_{xy}$ で記号 $y \in \mathcal{Y}$ が出力されることを表しています。確率の定義より任意の $x \in \mathcal{X}$ に対して $\sum_{y \in \mathcal{Y}} P_{xy} = 1$ が成り立ちます。

送信者と受信者は通信路についての情報（特に通信路行列）をお互い知っています。まず、両者は協議しながら符号化関数 $f\colon \mathcal{M} \to \mathcal{X}^K$ と復号関数 $g\colon \mathcal{Y}^K \to \mathcal{M}$ を設計します。$K \in \mathbb{Z}_+$ は一つもメッセージをいくつの通信路記号に置き換えるかを表す整数です。

続いて両者は遠隔地に離れます。送信者がメッセージ $m \in \mathcal{M}$ を送信するとき、$f(m) = x_1 x_2 \cdots x_n$ を通信路に入力し、受信者はメッセージ $y = y_1 y_2 \cdots y_n$ を受信し、$g(y)$ により復号します。ここで、$y_i$ は通信路確率 $p(y \mid X = x_i) = P_{y x_i}$ により確率的に定まります。$y_i$ は $x_j ~(j \neq i)$ とは独立であることに注意してください。$m = g(y)$ となれば通信成功です。

$m \in \mathcal{M}$ が一様に選ばれるとしたとき、通信が失敗する確率 $\frac{1}{n} \sum_{m \in \mathcal{M}} p(m \neq g(y) \mid M = m)$ を小さく抑えつつ、通信に必要な記号の個数 $K$ を小さく抑えるのが目標です。

例: 二元対称通信路

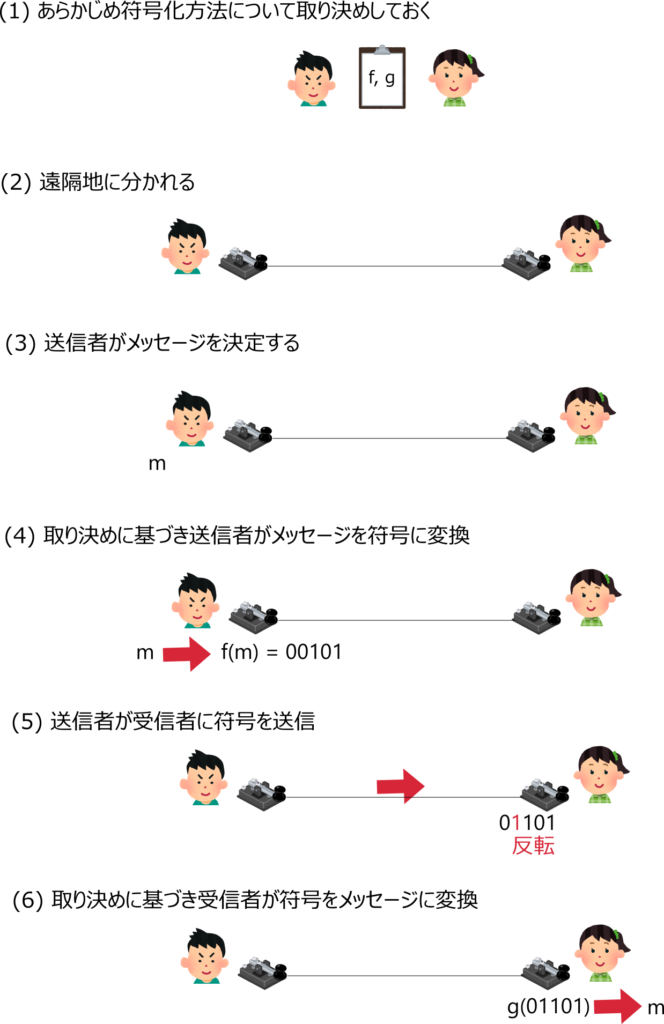
二元対称通信路は最も単純な通信路の例です。二元対称通信路の入出力記号は$\mathcal{X} = \{0, 1\}, \mathcal{Y} = \{0, 1\}$ の二元のみであり、通信路行列は実数 $p \in [0, 1]$ を用いて以下で表されます。$$P = \begin{pmatrix} 1-p & p \\ p & 1-p\end{pmatrix}$$ つまり、確率 $p$ で記号が反転して伝えられるということです。$p$ が現実的な通信路では非常に小さい場合が多いですが、衛星通信などノイズの多い場合には $0.5$ に近い値を取る場合もあります。$p = 1.0$ の時には常に反転するということなので、読み手の方で反転させれば常に通信が成功する信頼度の高い通信路と見做せることに注意してください。

例: 二元対称消失通信路

二元対称消失通信路の入出力記号は $\mathcal{X} = \{0, 1\}, \mathcal{Y} = \{0, \bot, 1\}$ であり、通信路行列は実数 $p, p_\bot \in [0, 1]$ を用いて以下で表せます。$$P = \begin{pmatrix} 1-p-p_\bot & p_\bot & p \\ p & p_\bot & 1-p-p_\bot\end{pmatrix}$$ つまり、確率 $p$ で記号が反転して伝えられ、確率 $p_\bot$ で通信が消失したことを表す記号 $\bot$ が伝えられます。消失というと、全く記号が届かないことを想像するかもしれませんが、通信は同期されているとし、消失した場合は消失したとわかります。たとえば、$x = 01010101$ を送信し、二文字目と三文字目が消失すると、受信者の元には $010101$ ではなく $0\bot\bot10101$ が届きます。通信が同期されていないときには、信号が届かない場合、送ったのかさえ分からない場合もありますが、標準的な通信路符号化の設定ではそのような場合は考えません。