符号の中には瞬時符号とよばれる望ましい性質をもつ符号が存在します。クラフトの不等式は、瞬時符号を構成するための条件を与える定理です。
情報源記号を \(\mathcal{X} = \{A, B, C\}\) の三種類、符号アルファベットを \(\Sigma = \{0, 1\}\) の二種類とします。
情報源記号・符号アルファベットを 0 個以上並べた集合を \(\mathcal{X}^* = \{\varepsilon, A, B, C, AA, AB, AC, BA, \cdots\}, \Sigma^* = \{\varepsilon, 0, 1, 00, 01, 10, 11, 000, 001, \cdots\}\) とします。ただし、 \(\varepsilon\) は空文字です。\(|\cdot|\) を文字列長とします。たとえば \(|AABA| = 4\) です。
符号化方法 \(f\colon \mathcal{X} \to \Sigma^*\) とすると、記号の濫用として、\(x^* = x_1 x_2 \cdots x_n \in \mathcal{X}^*\) について \(f(x) = f(x_1) f(x_2) \cdots f(x_n)\) と定義します。たとえば \(f(A) = 001, f(B) = 111\) とすると \(f(AAB) = 001001111\) です。
\(f(A) = 0, f(B) = 0, f(C) = 1\) という符号を考えます。この符号は非常に短いですが、異なる情報源記号が同じ符号に割り当てられているため、正しく復号ができません。たとえば、「0」という符号系列が送られてきた時、もとのメッセージが A であったのか B であったのかが分かりません。これを避けるのが非特異符号です。
もちろん、符号は非特異であることが望ましいです。
\(f(A) = 0, f(B) = 01, f(C) = 1\) という符号を考えます。異なる情報源記号には異なる符号語が割り当てられているので、この符号は非特異です。しかし、受信した符号系列が \(01\) であったとき、もとのメッセージが AC であったのか B であったのか分かりません。これを避けるのが一意復号可能符号です。
もちろん、符号は一意復号可能であることが望ましいです。
明らかに、一意復号可能であれば、非特異符号です。
$$\forall x^*, y^* \in \mathcal{X}^*, f(x^*) = f(y^*) \Rightarrow x^* = y^*$$ とすると、\(x^* = x, y^* = y\) ととれば、$$\forall x, y \in \mathcal{X}, f(x) = f(y) \Rightarrow x = y$$ が成立する。
\(f(A) = 111, f(B) = 1110, f(C) = 00\) という符号を考えます。これは一意復号可能符号になっています。\(111000000000\) は \(BCCCC\) と一意に復号されます。しかし、この符号系列を途中まで受信した際、\(ACCC…\) と続くのか、\(BCCC…\) と続くのかが一意に定まらず、最後まで系列を受信した時点でようやく符号が定まります。これを避けるのが瞬時符号です。
もちろん、符号は瞬時符号であることが望ましいです。
情報源記号に対応する場所まで受信するとその都度一意に復号できることを述べているので、これは、単に最後まで受信すれば一意であることを述べている一意復号可能符号よりも強い条件です。
$$\forall x^*, y^* \in \mathcal{X}^*, \forall w^* \in \Sigma^*, f(x^*)w^* = f(y^*) \Rightarrow x^* = y^*$$ とすると、\(w^* = \varepsilon\) ととれば、$$\forall x^*, y^* \in \mathcal{X}^*, f(x^*) = f(y^*) \Rightarrow x^* = y^*$$ が成り立つ。
\(f(A) = 111, f(B) = 1110, f(C) = 00\) という符号を考えます。\(f(A) = 111\) は \(f(B) = 1110\) の先頭三文字に一致します。このように、ある符号語 \(w\) が別の符号語 \(v\) の先頭の列に一致してしまうと、\(w\) を受信した時点で即情報源記号に対応するのか、続きを受信してから復号すればいいのかを定めることができません。よって、この場合は瞬時符号とはなりません。これを避けるのが接頭辞符号です。
もちろん、符号は接頭辞符号であることが望ましいです。
接頭辞符号でないなら瞬時符号でないことは上の議論から明らかです。逆に、接頭辞符号であれば、情報源記号に対応する場所まで受信するたび、情報源記号を確定させられるので、瞬時符号となります。
\(\Rightarrow\): $$\forall x^*, y^* \in \mathcal{X}^*, \forall w^* \in \Sigma^*, f(x^*)w^* = f(y^*) \Rightarrow x^* = y^*$$ とする。\(x^* = x, y^* = y\) ととると、$$\forall x, y \in \mathcal{X}, \forall w^* \in \Sigma^*, f(x)w^* = f(y) \Rightarrow x = y$$ が成り立つ。
\(\Leftarrow\): $$\forall x, y \in \mathcal{X}, \forall w^* \in \Sigma^*, f(x)w^* = f(y) \Rightarrow x = y \tag{1}$$とする。\(x^* = x_1, x_2, \cdots, x_n \in \mathcal{X}^*, y^* = y_1, y_2, \cdots, y_m \in \mathcal{X}^*\) に対して \(f(x^*) = f(y^*)\) であったとする。一般性を失うことなく \(|f(x_1)| \le |f(y_1)|\) を仮定する。このとき、仮定 (1)と \(f(x_1)w^* = f(y_1)\) より \(x_1 = y_1\) が成立。また、先頭の共通する記号を取り除くと \(f(x_2 \cdots x_n) = f(y_2 \cdots y_l)\) となるので、同様の議論により \(x_2 = y_2, \cdots, x_n = y_n, n = l\) と確定させられる。
これらの関係を図で表すと以下のようになります。
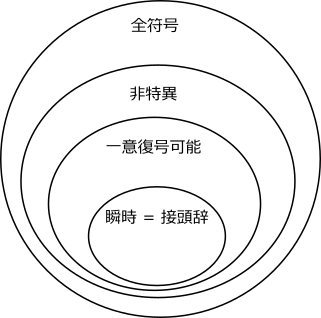
さまざまな符号のクラスのうち、瞬時符号 = 接頭辞符号が最も望ましい符号であることが分かりました。どのような条件のときに、どうすれば瞬時符号でかつ短い符号を構築できるのでしょうか。それを明らかにするのが符号の木とクラフトの不等式です。
符号の木は、符号化方法を樹形図で表したものです。符号の木は空文字からはじまり、情報源アルファベットを枝分かれさせたものです。たとえば、\(f(A) = 01, f(B) = 001, f(C) = 1\) に対応する深さ 3 までの符号の木は以下になります。
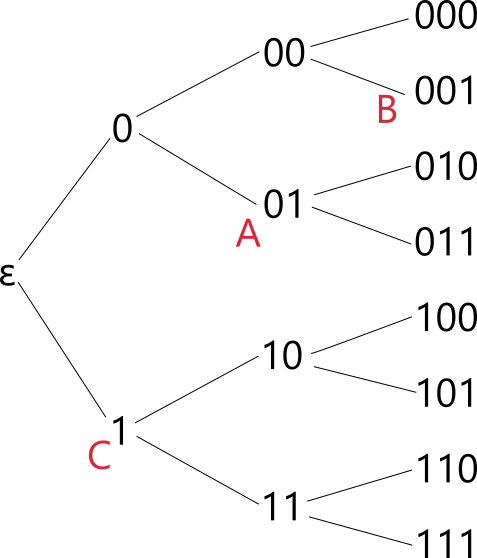
木についての用語を確認しておきましょう。最も深いレベルにある頂点を葉といいます。頂点について、その頂点の先にある全ノードを部分木といいます。
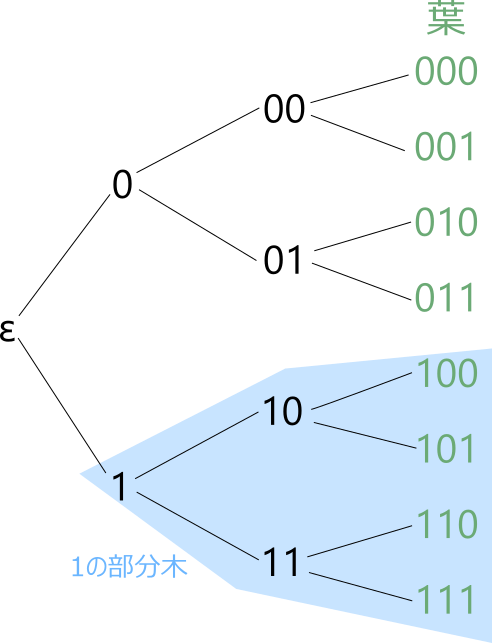
クラフトの不等式は、瞬時符号を構成するための符号語の長さの条件を示します。
\(2^{-|(f(x)|}\) の基数が \(2\) であるのは、符号アルファベットが \(2\) であるからです。一般には基数は符号アルファベットの大きさとなります。
\(\Rightarrow\): \(f\) を瞬時符号とし、\(L = \max_{x \in \mathcal{X}} |f(x)|\) を符号語の最大長とする。深さ \(L\) の符号の木を考える。各情報源記号 \(x \in \mathcal{X}\) について、\(f(x)\) に対応する頂点の部分木に印を付ける。接頭語符号性より、同じ頂点は二度印を付けられることがない。また、\(f(x)\) の部分木には \(2^{L – |f(x)|}\) 個の葉が含まれる。葉は全体で \(2^L\) 個しかないので、$$\begin{align*} \sum_{x \in \mathcal{X}} 2^{L – |f(x)|} &\le 2^L \\ \sum_{x \in \mathcal{X}} 2^{- |f(x)|} &\le 1 \end{align*}$$ が成り立つ。
\(\Leftarrow\): \(l \in \mathbb{N}^\mathcal{X}\) に対して $$\sum_{x \in \mathcal{X}} 2^{-l_x} \le 1 \tag{1}$$ が成り立つとする。一般性を失うことなく、\(\mathcal{X} = \{1, 2, \cdots, n\}\) かつ \(l_1 \le l_2 \le \cdots \le l_n\) であると仮定する。深さ \(l_n\) の印のない符号の木を構築し、\(i = 1, \cdots, n\) に対して順番に、深さ \(i\) のまだ印が付けられていない頂点を \(i\) の符号語とし、部分木全ての頂点に対して印をつける。構成法より明らかに接頭辞符号である。また、\(i\) の符号語を構築する際、深さ \(l_i\) の既に印の付いた頂点の数は $$\begin{align*} \sum_{k = 1}^{i-1} 2^{l_i – l_k} &= \left(\sum_{k = 1}^{n} 2^{l_i – l_k}\right) – \left(\sum_{k = i}^{n} 2^{l_i – l_k}\right) \\ &\le \left(\sum_{k = 1}^{n} 2^{l_i – l_k}\right) – \left(\sum_{k = i}^{i} 2^{l_i – l_k}\right) \\ &= \left(\sum_{k = 1}^{n} 2^{l_i – l_k}\right) – 1 \\ &= \left(2^{l_i} \sum_{k = 1}^{n} 2^{- l_k}\right) – 1 \\ &\le 2^{l_i} – 1\end{align*}$$ である。ただし、最後の不等式では式 (1) を用いた。よって、\(i\) の符号語を構築する際、深さ \(l_i\) には常にまだ印の付いていない頂点があるので、常にこのような符号は構成できる。
証明の後半は構成的に示しています。以下に、\(l_A = 1, l_B = 2, l_C = 3, l_D = 3\) の場合の構築方法を示します。

- 符号には、非特異符号・一意復号可能符号・瞬時符号・接頭語符号などのクラスがある
- 瞬時符号(= 接頭語符号)が最も望ましい
- クラフトの不等式は瞬時符号の符号語の長さの必要十分条件を与える


