この章では、言語から新しい言語を生み出す正規演算について学びます。
正規演算は和集合演算、連結演算、スター演算からなります。
和集合演算はその名の通り、二つの言語の和集合を取ります。直感的には、二つの言語のうちどちらかに含まれている文字列全体を表します。
言語 \(A\) と言語 \(B\) の和集合を \(\{A \cup B = \{w \mid w \in A \lor w \in B\}\) と表す。
例えば \(A = \{000, 00\}, B = \{111, 11\}\) とすると \(A \cup B = \{000, 00, 111, 11\}\) となります。また \(A\) を「00010を一部に含む文字列全体の集合」、\(B\) を「01110を一部に含む文字列全体の集合」とすると、\(A \cup B\) は「00010 または 01110 を一部に含む文字列全体の集合」となります。
連結演算は、二つの言語に含まれる文字列のあらゆる組合せを連結した全体の集合です。まず文字列の連結について定義します。
文字列 \(w = w_1 w_2 \cdot w_n\) と \(v = v_1 v_2 \cdots v_m\) の連結を \(w v = w_1 w_2 \cdots w_n v_1 v_2 \cdots v_m\) と表す。
例えば \(w = 000, v = 11\) とすると \(wv = 00011\) です。言語の連結は以下で定義されます。
言語 \(A\) と言語 \(B\) の連結を \(\{A \circ B = \{wv \mid w \in A \land v \in B\}\) と表す。
一般に \(A \odot B \neq B \odot A\) であることに注意してください。
例えば \(A = \{000, 00\}, B = \{111, 11\}\) とすると \(A \circ B = \{000111, 00111, 00111, 0011\}\) となります。また \(A\) を「00010を一部に含む文字列全体の集合」、\(B\) を「01110を一部に含む文字列全体の集合」とすると、\(A \circ B\) は「00010 の後に 01110 が出現する文字列全体の集合」となります。文字集合を英字全体として \(A = \{good, bad\}, B = \{boy, girl\}\) とすると \(A \circ B = \{goodboy, goodgirl, badboy, badgirl\}\) となります。
スター演算とは、言語から任意個の要素を重複ありで取り出し連結したもの全体の集合です。
言語 \(A\) に対するスター演算を \(A^* = \{w_1 w_2 \cdots w_n \mid n \in \mathbb{N}, w_i \in A\) と表す。
スター演算においてはゼロ個の連結も許されることを注意してください。つまり、スター演算の結果には空文字列が必ず含まれます。例えば \(A = \{00, 111\}\) とすると \(A^* = \{\varepsilon, 00, 111, 0000, 00111, 11100, 111111, 000000, 0000111, 0011100\), \(00111111, 1110000, 11100111, 11111100, 111111111, 00000000, \cdots\}\) となります。また、また \(A\) を「00010を一部に含む文字列全体の集合」とすると\(A^* = A \cup \{\varepsilon\}\) となります（なぜだか考えてみてください）。
以上の三つの演算をまとめて正規演算といいます。
和集合演算、連結演算、スター演算をまとめて正規演算という
ある集合の要素に演算を施したとき、演算結果が常にその集合内に収まるとき、演算が閉じていると言います。以上で導入した正規演算は正規言語について閉じています。このことを示します。数学的に厳密な議論は煩雑になりすぎるので、ここでは図を使った証明を行います。
正規言語 \(A, B\) について \(A \cup B\) は正規言語
\(A\) を認識する非決定性有限オートマトン \(M\) と \(B\) を認識する非決定性有限オートマトン \(N\) が存在する。以下のように、新しい開始状態から \(M\) と \(N\) の開始状態に \(\varepsilon\) 矢印が伸びている非決定性有限オートマトン \(P\) を用意する。
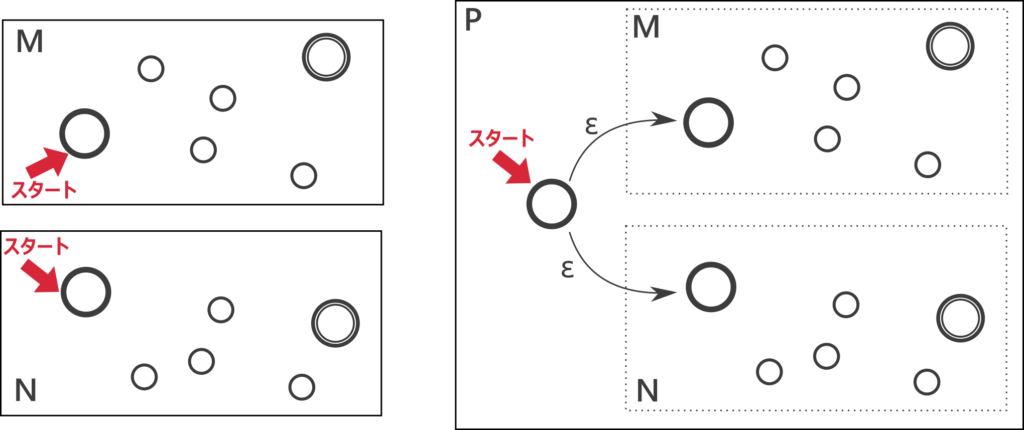
文字列 \(w \in A\) については、最初 \(\varepsilon\) で上側に遷移すれば \(M\) は \(w\) を受理するので \(P\) も \(w\) を受理する。
文字列 \(w \in B\) については、最初 \(\varepsilon\) で下側に遷移すれば \(N\) は \(w\) を受理するので \(P\) も \(w\) を受理する。
よって、\(P\) は \(A \cup B\) の全ての要素を受理する。
逆に、\(P\) が文字列 \(w\) を認識したとする。受理する状態遷移において最初の遷移が上側の矢印であれば、構成方法より \(M\) も \(w\) を受理するので \(w \in A\)。すなわち \(w \in A \cup B\)。最初の遷移が下側の矢印であれば、構成方法より \(N\) も \(w\) を受理するので \(w \in B\)。すなわち \(w \in A \cup B\)。
よって、\(P\) が受理する文字列は \(A \cup B\) の要素に限る。
以上より \(P\) は \(A \cup B\) を認識する。\(A \cup B\) は非決定性有限オートマトンに認識されるので正規言語。
正規言語 \(A, B\) について \(A \circ B\) は正規言語
\(A\) を認識する非決定性有限オートマトン \(M\) と \(B\) を認識する非決定性有限オートマトン \(N\) が存在する。以下のように、\(M\) と \(N\) を並べて \(M\) の受理状態から \(N\) の開始状態に \(\varepsilon\) 矢印を伸ばした非決定性有限オートマトン \(P\) を用意し、\(N\) の受理状態のみを \(P\) の受理状態とする。
文字列 \(w \in A, v \in B\) について \(wv\) を \(P\) に入力すると \(w\) を読み終わった時点で \(M\) の受理状態に遷移でき、そこから \(\varepsilon\) 矢印で \(N\) の開始状態に遷移できる。そこから \(v\) を読んで \(N\) の受理状態に遷移できるので、\(P\) は \(wv\) を受理する。
逆に、文字列 \(u\) が \(P\) に受理されたとすると、どこかのタイミングで \(M\) から \(N\) への \(\varepsilon\) 矢印を辿ったはずである。その時点ですでに読まれた文字列を \(w\) とし \(u = wv\) と分解すると、構成方法より \(M\) は \(w\) を受理し、\(N\) は \(v\) を受理する。よって \(u \in A \circ B\)
以上より、 \(P\) は \(A \circ B\) を認識する。
正規言語 \(A\) について \(A^*\) は正規言語
\(A\) を認識する非決定性有限オートマトン \(M\) が存在する。以下のように、新しい初期状態から \(M\) の開始状態に \(\varepsilon\) 矢印を伸ばし、\(M\) の受理状態から \(M\) の開始状態に \(\varepsilon\) 矢印を伸ばした非決定性有限オートマトン \(P\) を用意する。\(M\) の受理状態と新しい開始状態を \(P\) の受理状態とする。
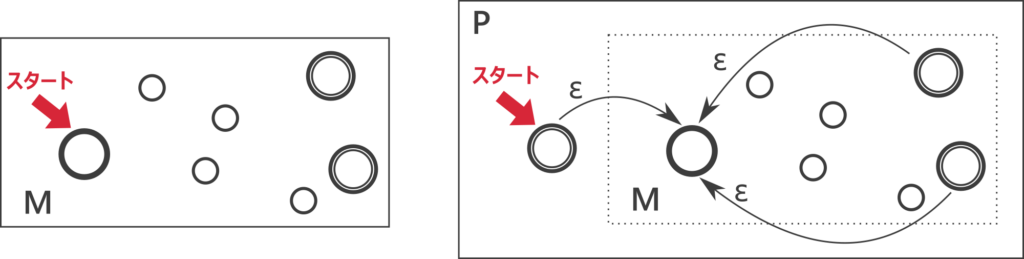
明らかに \(P\) は \(\varepsilon\) を受理する。
文字列 \(w_1, w_2, \cdots, w_n \in A\) について \(w = w_1 w_2 \cdots w_n\) を \(P\) に入力すると \(w_1\) を読み終わった時点で \(M\) の受理状態に遷移でき、そこから \(\varepsilon\) 矢印で \(M\) の開始状態に遷移できる。そこから \(w_2\) を読んで \(M\) の受理状態に遷移できる。これを繰り返して、\(w_n\) を読んだあと \(M\) の受理状態に遷移できるので \(P\) は \(w\) を受理する。
逆に、\(w \neq \varepsilon\) を \(P\) が受理したとすると、受理した状態列において \(M\) の受理状態から開始状態への \(\varepsilon\) 矢印を辿ったタイミングで読み込んだ文字列で区切り \(w = w_1 w_2 \cdots w_n\) と分割すると、構成方法から各 \(w_i\) は \(M\) によって受理される。よって \(P\) が受理する文字列は \(A^*\) の要素のみ。
以上より、 \(P\) は \(A^*\) を認識する。
- 二つの言語の和集合を取るのが和集合演算
- 二つの言語のあらゆる組を連結したもの全体を表すのが連結演算
- 一つの言語の要素を繰り返し並べたもの全体を表すのがスター演算
- 正規言語については、これらの演算を適用した結果も正規言語となる
正規演算と正規表現が似ていることに気づいた方もいるかもしれません。正規演算は正規表現の理論の基礎となっています。次章では正規表現について学びます。
