非決定性有限オートマトン: 形式言語理論入門 6

ここまでは決定性有限オートマトンを見てきましたが、この章では、非決定有限オートマトンを定義します。

非決定性有限オートマトン

まず、決定性有限オートマトンの時のように、図を使って直感的な説明をします。非決定性有限オートマトンは以下の図のように表されます。

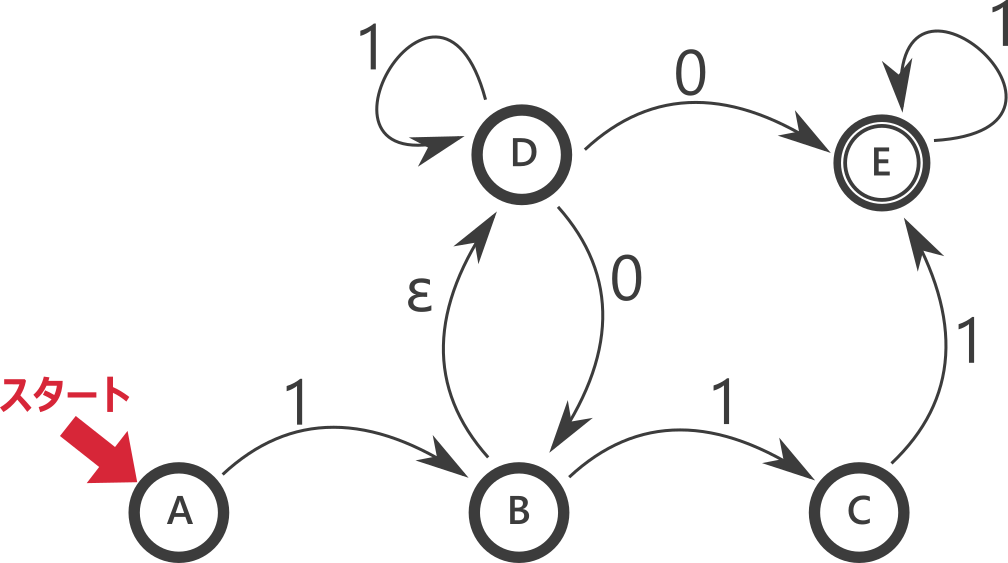
決定性有限オートマトンとずいぶん似ていますが、異なる点が二つあります。一つ目は、一つの状態から出る同じ文字の矢印が一つとは限らないこと。例えば上の例では状態 C から 0 の矢印が二本出ていて、1 の矢印は一本も出ていません。二つ目は、\(\varepsilon\) と書かれている矢印があることです。

非決定性有限オートマトンはどのように動作するのでしょうか。非決定性有限オートマトンにおいて、同じ文字の矢印が二つ以上ある場合、どの矢印を選んでもよいです。また、\(\varepsilon\) の矢印は文字を読むことなく、たどってもよいし、たどらなくてもよいです。遷移の仕方が一通りに定まらないことが「非決定性」という名前の由来です。

非決定性有限オートマトンではたどり方が複数あるわけですが、受理状態にたどり着くようなたどり方が一つでもあるならば非決定性有限オートマトンはその文字列を受理します。

具体例で考えてみましょう。例えば、上の非決定性オートマトンにおいて、入力が 101 だとしましょう。初期状態はAです。ここから文字1を読み取り状態Bに移ります。状態Bから \(\varepsilon\) の矢印があるのでたどり状態Dに移るとしましょう。次の文字は0ですが二つ選択肢があります。下に向かう矢印をたどり状態Bに移ったとしましょう。次の文字は1で状態Cに移ります。これは受理状態ではないです。しかし、これでこのオートマトンが文字列 101 を受理しないと決まったわけではありません。たどり方がまずかっただけかもしれないからです。実際、文字1で状態Bに移り、\(\varepsilon\) で状態Dに移り、文字0で状態Eに移り、文字1で状態Eに移ると受理状態なので、このこのオートマトンは文字列101を受理します。

次は入力が110だとしましょう。一文字目で状態Bに移り、二文字目で状態Cに移るとします。三文字目は0ですが状態Cからは辿るべき矢印が出ていません。この場合はこのたどり方では受理されません。しかし、やはりたどり方が悪かっただけかもしれません。今度は一文字目で状態Bに移り、\(\varepsilon\) の矢印を辿り状態Dに移り、二文字目で状態Dに移り、三文字目で状態Eに移ると受理されます。

入力が001だとしましょう。一文字目でいきなり辿るべき矢印がありません。この場合はどうしても受理状態までたどり着けないのでこのオートマトンは 001 を受理しません。

非決定性有限オートマトンの何が良いのか

すでに決定性有限オートマトンを学んだ我々が非決定性有限オートマトンを学ぶ利点は何でしょうか。非決定性有限オートマトンの受理条件は複雑で、一見扱いづらそうに見えます。しかし、非決定性有限オートマトンは決定性有限オートマトンに比べて、所望の言語を表現するオートマトンを簡単に構築できることが多いです。

例えば、「00010 または 01110 を一部に含む文字列全体の集合」という言語を考えてみましょう。たとえば 111000100 は 4 文字目から 8 文字目に 00010 を含むのでこの言語の要素であり、0011100010 は 2 文字目から 6 文字目に 01110 を含むのでこの言語の要素です（6 文字目から 10 文字目に 00010 も含みます）。このような言語は検索エンジンの OR 検索を実現するときに重要になります。

実はこの言語を表現する決定性有限オートマトンを構築するのは難しいです。（難しいことを示すのはできないですが、作ろうとチャレンジしてみると難しいと分かると思います。）

一方、この言語を表現する非決定性有限オートマトンは以下のように簡単に構築できます。

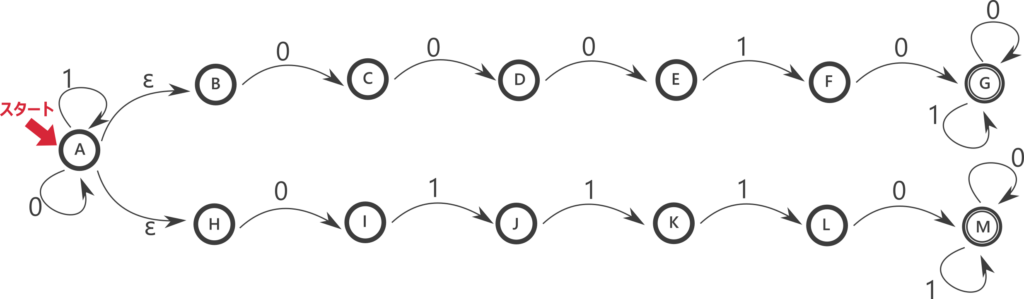
初期状態から上側の道と下側の道に分岐したような形になっています。直感的には上側の道が 00010 に対応し、下側の道が 01110 に対応します。

開始状態からは 0 と 1 の矢印が自身に向かって伸びているので、いくらでも開始状態にとどまることができます。また、開始状態から上側と下側の道に \(\varepsilon\) の矢印が伸びているので、好きなタイミングで道に移ることができます。入力文字列に 00010 または 01110 が含まれていればその部分で道に移れば右端の受理状態まで遷移することができます。例えば 111000100 の場合、3 文字目までは開始状態にとどまり、4 文字目を読み取る直前で \(\varepsilon\) 矢印を辿って上側の状態に遷移し、4, 5, 6, 7, 8 文字目で右に進み残りを右上の状態にとどまっておけるので、受理されます。一方、00010 も 01110 も含まない入力文字列では、どのタイミングで道に移っても右端まで辿ることができないので受理されません。

このように、どこか分からないけどどこかに文字列が含まれるようなもの全てを受理したい場合、非決定性が有効になります。「00010 または 01110」というのも、どちらかが含まれているか分からないということなので非決定性の例になります。

他にも、上記のオートマトンの右端の受理状態において、自分自身への矢印を取り去ると、「00010 または 01110 で終わる言語」を表現することができます。

このように、非決定性有限オートマトンは様々な言語を簡潔かつ直感的に表現することができるのです。

非決定性有限オートマトンの定義

非決定性有限オートマトンの定義を数学的に述べます

定義: 非決定性有限オートマトン

非決定性有限オートマトンとは五つ組 \((\Sigma, Q, \delta, q_0, F)\) である。ただし、\(\Sigma\) は文字を表す有限集合、\(Q\) は状態を表す有限集合、\(\delta\colon Q \times (\Sigma \cup \{\varepsilon\}) \to 2^Q\) は遷移関数、\(q_0 \in Q\) は初期状態、\(F \subseteq Q\) は受理状態である。

決定性有限オートマトンの場合とほとんど同じですが、遷移関数の定義域と値域が異なります。\(\varepsilon\) が書かれた矢印があることから分かるように、遷移関数の文字の部分には \(\varepsilon\) も取ることができるようになっています。また、\(2^Q\) は \(Q\) のべき集合（部分集合全体の集合）です。\(\delta(q, c)\) は状態 \(q\) で文字 \(c\) を受け取ったときに遷移できるさきの状態集合を表しています。矢印が内場合、つまり遷移できる先がない場合は空集合になります。例えば上の例の場合、\(\delta(A, 1) = \{B\}\), \(\delta(D, 0) = \{B, E\}\), \(\delta(A, 0) = \emptyset\) となります。

非決定性有限オートマトンが受理する言語

非決定性有限オートマトンが受理する言語を数学的に定義します。

定義: 非決定性有限オートマトンの受理

決定性有限オートマトン \(M = (Q, \Sigma, \delta, q_0, F)\) は文字列 \(w = w_1 w_2 \cdots w_n \in \Sigma^*\) を以下の条件を満たすとき受理する。

ある文字列 \(y = y_1 y_2 \cdots w_m \in (\Sigma \cup \{\varepsilon\})*\) と状態の列 \(r_0, r_1, \cdots, r_m \in Q\) が存在し、以下の四条件が成り立つ。

\(y\) から \(\varepsilon\) を全て取り除くと \(w\) に一致する
\(r_0 = q_0\) (初期状態)
\(r_i \in \delta(r_{i-1}, y_i), \forall i = 1, 2, \cdots, m\) (正しく遷移する)
\(r_m \in F\) (最終状態は受理状態)

非決定性有限オートマトンでは \(\varepsilon\) の矢印を好きなタイミングでたどれます。入力文字列 \(w\) に \(\varepsilon\) をたどるタイミングを挿入した文字列が \(y\) です。例えば、入力が \(w = 101\) のとき、一文字目を読み込んだあと（だけ）で \(\varepsilon\) の矢印をたどるのであれば \(y = 1\varepsilon01\) となります。\(r_i\) はこの拡張した文字列上で \(i\) 文字目まで読み込んだときの状態に対応します。遷移先は複数ある場合がありますが、\(r_i \in \delta(r_{i-1}, y_i)\) はそのうちのどれか一つに遷移していることを表しています。受理状態にたどりつく \(\varepsilon\) の挿入の仕方やたどり方が一つでもあれば非決定性有限オートマトンは入力文字列を受理することを表しています。

非決定性有限オートマトンにおいても同様に、オートマトン \(M\) が受理する文字列全体の集合を \(L(M) = \{w \in \Sigma^* \mid M \text{ は } w \text{ を受理する }\}\) と表し、言語 \(A \subset \Sigma^*\) が \(L(M)\) に一致するとき、オートマトン \(M\) は言語 \(A\) を認識するといいます。

前回の流れからいえば、正規言語のように、非決定性有限オートマトンが認識できる言語の集合に名前をつけたいところですが、実は次の章でみるように、非決定性有限オートマトンが認識できる言語は正規言語に一致します。非決定性有限オートマトンが決定性有限オートマトンよりも複雑になりできることが増えていることを考えると驚くべきことです。