この章では、形式言語というものを改めて数学的に定義し、決定性有限オートマトンが表す言語を定義します。
まずは基本となる文字列の定義です。
文字集合 \(\Sigma\) の要素の長さ 0 以上の列を文字列といい、文字列全体の集合を \(\Sigma^*\) で表す。
例えば \(\Sigma = \{0, 1\}\) のとき、0001 や 0101110110 は文字列です。
「長さ 0 以上」という部分に注意してください。何にも並んでいない列も文字列だと定義します。この特殊な文字列を空文字列（からもじれつ、または、くうもじれつ）と呼び、\(\varepsilon\) と表します。空文字列は、集合でいうところの空集合、数でいうところのゼロに相当します。\(\varepsilon\) という記号は空集合が \(\emptyset\) で表現されたことに相当します。
次に言語を定義します。以降、言語というと全て形式言語を指します。
文字列の集合を言語という。すなわち、言語とは \(\Sigma^*\) の部分集合である。
例えば \(\{0001, 0101110110\}\) や「1を偶数個含む文字列の集合」は言語です。前者は有限集合、後者は無限集合ですが、どちらも言語です。
「1を偶数個含む文字列の集合」のように定義を日本語で書き表すときには空文字列が含まれるかどうかを見落としがちなので注意しましょう。空文字列には1がゼロ個、つまり偶数個含まれていることを考えると空文字列もこの言語に含まれると考える方が自然です。ですが、空文字列を含まないつもりで定義してしまっている場合もあります。慣れないうちは、「1を偶数個含む文字列の集合（空文字列含む）」や「1を偶数個含む文字列の集合（空文字列を除く）」のように明示すると間違いが少ないです。
決定性有限オートマトンが表す言語を数学的に定義します。これは厳密に書くとややこしいですが、丸と矢印の図でオートマトンを動かすイメージをもって読むと理解しやすいです。
決定性有限オートマトン \(M = (Q, \Sigma, \delta, q_0, F)\) は文字列 \(w = w_1 w_2 \cdots w_n \in \Sigma^*\) について、\(q_i = \delta(q_{i-1}, w_i) ~ (i = 1, 2, \cdots, n)\) と定義すると、\(q_n \in F\) であるときオートマトン \(M\) は \(w\) を受理するという。
ここで、\(q_i\) は \(i\) 番目の文字まで読み込んだときにいる状態に相当します。\(q_n\) は最終状態を表し、これが受理状態であればオートマトンはこの文字列を受理します。
オートマトン \(M\) が受理する文字列全体の集合を \(L(M) = \{w \in \Sigma^* \mid M \text{ は } w \text{ を受理する }\}\) と表す。言語 \(A \subset \Sigma^*\) が \(L(M)\) に一致するとき、オートマトン \(M\) は言語 \(A\) を認識するという。
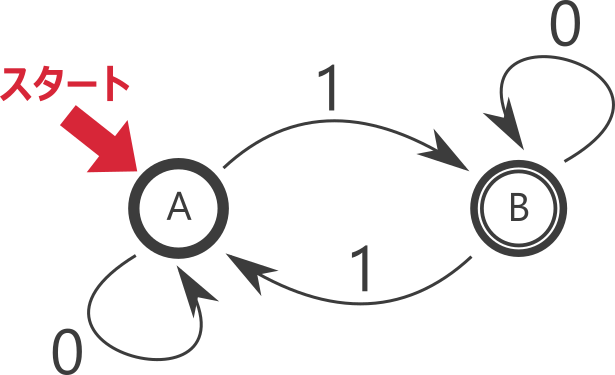
たとえば、以前の例でみた以下の図で表されるオートマトンは「1を奇数個含む文字列全体」を認識します。
決定性有限オートマトンが認識する言語の集合を正規言語といいます。厳密に述べると以下のようになります。
言語 \(A\) は、ある決定性有限オートマトン \(M\) が存在し、\(M\) が \(A\) を認識するとき正規言語であるという。
たとえば、「0を奇数個含む文字列全体」や「0を三つ連続で含む文字列全体」は、以前みたようにこれらを認識する決定性有限オートマトンが存在するので正規言語です。
ネタバレとなりますが、正規言語は正規表現が表現できる言語全体と同じになることをこの後の章で見ます。
この定義を逆に読むと、正規言語でなければ、どれだけ頑張ってもその言語を認識する決定性有限オートマトンは作れません。以降の章では、どのような条件を満たす言語が正規言語になるのかを探っていきます。
- 文字の列を文字列という
- 文字列部分集合を言語という
- 決定性オートマトンが認識できる言語を正規言語という
