最も基本的なオートマトンである決定性有限オートマトンについて学んでいきます。数学的な定義は次の章に回すことにして、この章では決定性有限オートマトンがどのようなものかを直感的に理解することをめざします。
前の章までは、「コンピュータ」を含む文字列、のようにひらがな・カタカナ・漢字の文字列の集合を考えてきましたが、これでは文字の種類が多くて扱いづらいので、今後は0と1からなる文字列を主に考えます。例えば、「”001010″を含む文字列全体の集合」のような感じです。”1100101010″はこの言語に含まれ、”01001101″は含まれません。アスキーコードやユニコードでエンコーディングされていると思えば、01文字列だけでも実質的にはアルファベット・ひらがな・カタカナ・漢字も扱うことができます。
決定性有限オートマトンは次のような丸と矢印の図で表されます。丸のことを状態とよびます。丸の中に書かれているアルファベットは状態の名前を表し、動作には影響しません。
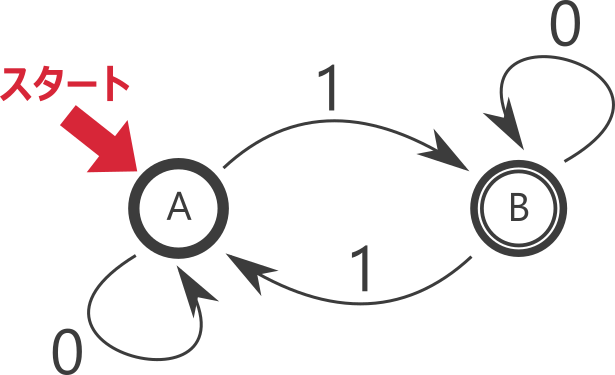
前章で話したように、オートマトンは文字列を受け取ると「はい」か「いいえ」を出力します。決定性有限オートマトンはどのようにこれを決定するのでしょうか。
決定性有限オートマトンは入力された文字列を一文字ずつ読み取っていきます。まず「スタート」と書かれている状態からはじめます。現在の状態から伸びている矢印のうち、入力文字列の一文字目と同じものを使って矢印の先の状態に移動します。次に、現在の状態から伸びている矢印のうち、二文字目と同じものを使って矢印の先の状態に移動します。三文字目、四文字目、と繰り返し、最後の文字を使って移った先の状態が二重丸で表される状態であれば「はい」、そうでなければ「いいえ」を出力します。途中で二重丸の状態を通ったとしても、最後の状態が二重丸でなければ「いいえ」を出力することに注意してください。すごろくをイメージすると分かりやすいと思います。
「はい」を出力することを受理する、「いいえ」を出力することを拒否するといいます。
例えば上のオートマトンので入力が”100101″の場合、状態Aからはじめて、A→B→B→B→A→A→Bと移り、最終状態Bが二重丸なので受理されます。
入力が”00101″の場合、A→A→A→B→B→Aと移り、最終状態Aが二重丸でないので拒否されます。
このオートマトンは1を受け取るたびに交互に状態が移ることを考えると、「1を奇数個含む全ての文字列」に相当する言語を表していることが分かります。
逆に、先に言語が決まっているとき、その言語を表す決定性有限オートマトンを考えてみましょう。例として「連続する三つの0を含む文字列」を考えます。直感的には、0を読み取るとカウントアップしていって、3つたまると受理するようなオートマトンがよさそうです。ただし、0は連続する必要があるのでカウントアップの途中で1が挟まると振り出しに戻る必要があります。これを形にすると以下のようになります。
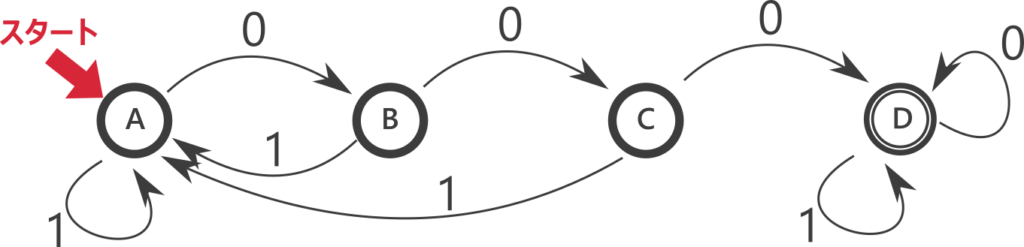
入力が00100001のとき、状態はA→B→C→A→B→C→D→D→Dとなり、二重丸で終わるので受理されます。
入力が0100101のとき、状態はA→B→A→B→C→A→B→Aとなり拒否されます。
たしかに正しく動いていそうです。
- 決定性有限オートマトンは丸と矢印の図で表され、入力文字列から一文字ずつ文字を読み取って状態を移っていき、最終状態が二重丸で表される状態であれば受理するモデル
次章からはこの決定性有限オートマトンを数学的に定義し、どのような言語が表せて、どのような言語が表せないのかといった、さまざまな性質を証明していきます。


