最後に、シンプレックス法と双対定理とビッグM法の有効性を実験を通して確認します。ランダムな入力例についてはシンプレックス法が非常に高速に動作することが分かります。
\(n = 1000\) 変数 \(m = 100\) 制約の標準形線形計画 $$\begin{align*}&\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad c^\top x \\ &\quad \text{s.t.} \qquad A x = b \\ &\qquad \qquad x \ge 0\end{align*}$$ のパラメータ \(c, A, b\) の要素を \([0, 1]\) の範囲の一様乱数から生成します。まずは、シンプレックス法がこの問題をどれほど高速に解けるか見てみます。
この問題の基底解は自明ではないので、ビッグM法で \(M = 1e6\) と置いてシンプレックス法を適用します。
シンプレックス法の各反復で見つかった解の目的関数値をプロットしたものが以下になります。
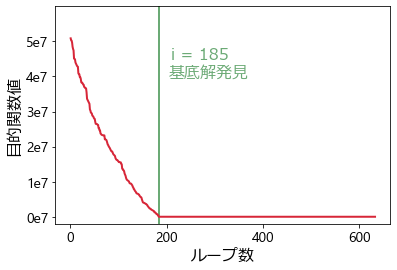
\(i = 185\) 回目の反復で \(M\) の成分が消えて目的関数値が大幅に減り、元の問題の基底解が見つかっています。以降の目的関数の値がよく見えないので下部にズームしたプロットを用意しました。
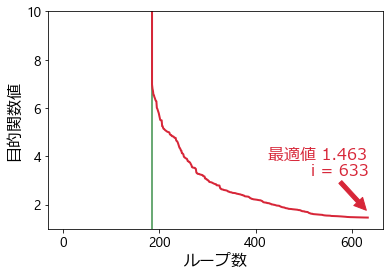
目的関数値は順調に下がり続け、全体の \(i = 633\) ループ目、基底解が見つかってから \(448\) 回のループで最適解が見つかりました。
有限回のステップで停止することを証明した際のループ回数のバウンドは \(_nC_m\) 回で、今回の場合は \(_{1000}C_{100} \approx 6 \cdot 10^{139}\) となります。このバウンドに比べて、実際は非常に高速に最適解が見つかっていることが分かります。
次に、この問題の双対問題 $$\begin{align*}&\underset{\lambda \in \mathbb{R}^{m}}{\text{maximize}} \quad b^\top \lambda \\ &\quad \text{s.t.} \qquad A^\top \lambda \le c\end{align*}$$ に対してシンプレックス法を適用しましょう。
各反復で見つかった解の目的関数値をプロットしたものが以下になります。
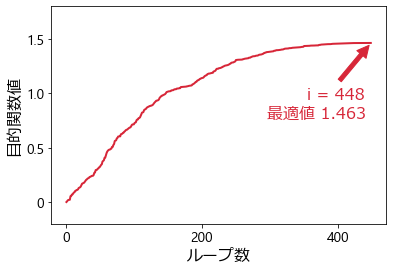
\(i = 448\) ループ目で最適解が見つかり、最適値は \(1.463\) です。最適値が主問題と一致していることが分かります。このことは強双対定理から保証されます。
- 線形計画をシンプレックス法を使って解いてみた
- シンプレックス法はランダムな問題例に対しては非常に高速に動作する
- 強双対定理が成り立つことを数値的に確かめた


