線形計画問題は目的関数が線形で実行可能領域が凸多面体な最適化問題です。
少し工夫をすると、目的関数が線形でなくても、区分線形・凸・連続の三条件さえ揃えば最小化問題を線形計画として定式化できることを紹介します。極限まで区分の数を増やすと一般の連続凸関数を目的関数とした最適化も線形計画として定式化できてしまいます。
区分線形関数とは、定義域がいくつかの区間に分かれ、それぞれの定義域内では一次関数であるものをいいます。
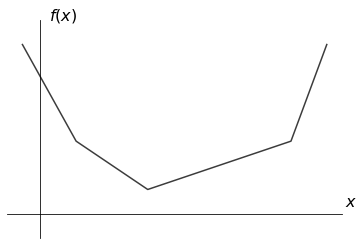
この記事では、区分線形な関数のうち、連続かつ凸なものを扱います。そのような関数は以下の性質を満たします。ここではこれを定義として扱います。
ベクトル \(a_1, a_2, \cdots, a_m \in \mathbb{R}^n\) と実数 \(b_1, b_2, \cdots, b_m \in \mathbb{R}\)を用いて $$f(x) = \max_{i = 1, \cdots, m} (a_i^\top x + b_i)$$ と表せる関数 \(f \colon \mathbb{R}^n \to \mathbb{R}\) を区分線形凸関数という。
上記の区分線形関数であれば、以下のように 4 つの一次関数の max で表されます。
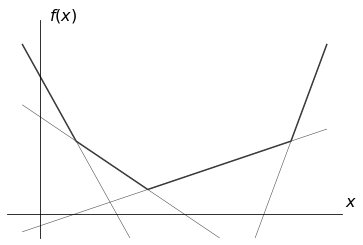
1 つの一次関数で表される区分線形凸関数として通常の線形関数が含まれるので、区分線形凸関数は線形関数よりも広い関数のクラスになります。
上記の一次元区分関数 \(f(x)\) を最小化する問題を考えます。ここで、決定変数に補助変数 \(t\) を加え、以下のようにグラフの上側を実行可能領域、目的関数を \(t\) とした最小化問題を考えます。
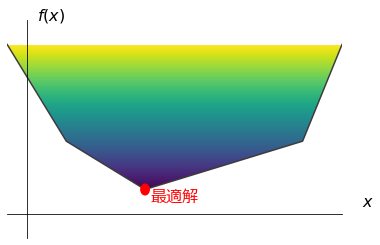
この問題は、目的関数が \(t\) なので一次関数、実行可能領域が凸多面体なので、線形計画で表せます。
上記の議論を一般化すると、
区分線形凸関数 $$f(x) = \max_{i = 1, \cdots, m} (a_i^\top x + b_i)$$ に最小解 \(x^*\) が存在するならば、$$\begin{align*}&\underset{(x, t) \in \mathbb{R}^{n+1}}{\text{minimize}} \quad t \\ &\quad \text{s.t.} \qquad a_1^\top x + b_2 \le t\\ &\qquad \qquad a_2^\top x + b_2 \le t \\ &\qquad \qquad \qquad \vdots \\ &\qquad \qquad a_m^\top x + b_m \le t\end{align*}$$ の最適値は \(f(x^*)\) に一致する。逆に、この線形計画に最小解 \((x^*_{\text{LP}}, t^*_{\text{LP}})\) が存在するならば、\(x^*_{\text{LP}}\) は \(f\) の最小解であり、\(t^*_{\text{LP}} = f(x^*_{\text{LP}})\) である。
順方向: 任意の実行可能解 \((x, t)\) について、$$f(x^*) \le f(x) = \max_{i = 1, \cdots, m} (a_i^\top x + b_i) \le t$$ が成り立つ。ここで、最初の不等式は \(x^*\) の最小性から、ふたつ目の不等式は線形計画の制約条件から従う。よって、線形計画問題の最適値は \(f(x^*)\) 以上である。
逆に、\(i = 1, 2, \cdots, m\) について \(a_i x^{*\top} + b_i \le f(x^*)\) が成り立つので、\((x^*, f(x^*))\) は実行可能解となり、線形計画の最適値は \(f(x^*)\) に一致する。
逆方向: 線形計画の制約条件より、$$f(x^*_{\text{LP}}) = \max_{i = 1, \cdots, m} (a_i^\top x^*_{\text{LP}} + b_i) \le t^*_{\text{LP}}$$ が成り立つ。この不等号が等号成立しないとすると、\((x^*_{\text{LP}}, f(x^*_{\text{LP}}))\) は実行可能なので最適性に反する。よって、\(f(x^*_{\text{LP}}) = t^*_{\text{LP}}\) が成り立つ。
また、仮に \(f(x’) < f(x^*_{\text{LP}})\) となる \(x’\) が存在したとすると、\((x’, f(x’))\) は実行可能であり \(f(x’) < f(x^*_{\text{LP}}) \le t^*_{\text{LP}}\) より最適性に反する。よって、\(x^*_{\text{LP}}\) は \(f\) の最小解である。
以上より、区分線形凸関数の最小化は、線形計画を解けば実現できます。
線形計画に最小解が存在すれば、逆方向より \(f\) の最小解がわかり、存在しなければ順方向の対偶より \(f\) に最小解が存在しないことがわかります。
区分線形凸関数というと、関数のクラスがかなり狭いように思うかもしれませんが、区間の区切り方をごくごく細かくしていけば、任意の凸関数を近似することができます。
細かいポリゴンで曲面を近似するようなイメージです。
例えば、二次元の場合だと以下のようになり、区分線形関数により表現される関数はほぼ曲面になります。
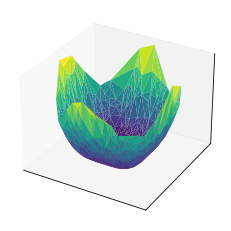
もちろん、あまりに区間を多くしすぎると対応する制約条件の数が多くなりすぎてしまい、効率的に解けなくなってしまいます。無理やり線形計画に帰着するよりも、凸関数として凸最適化アルゴリズムを適用する方が効率的である場合も多いです。
それでも、曲面を区分線形関数で近似できることは頭に入れておくと、線形計画モデリングの見通しが立ちやすくなる場合も多いです。
滑らかな凸集合や凸関数を区分線形関数で無理やり近似すると大抵効率が悪くなってしまいますが、近似の仕方をうまく選ぶことで効率よく解くアルゴリズムも存在します。その代表例が凸計画に対する平面切除法です。
凸計画に対する平面切除法は実行可能領域が凸集合である問題に対して適用できる最適化アルゴリズムです。まず、実行可能領域を含む単純な凸多面体を構築し、これを新たな実行可能解とした問題を線形計画で解き、得られた解が元の問題の実行可能領域の外（つまり凸多面体と元の実行可能解の間）にあれば、その解が線形計画の実行可能解から外れるように平面を追加して線形計画を解き直すことを繰り返します。もし得られた解が元の実行可能領域の中にあれば、これは元の問題の最適解になります。
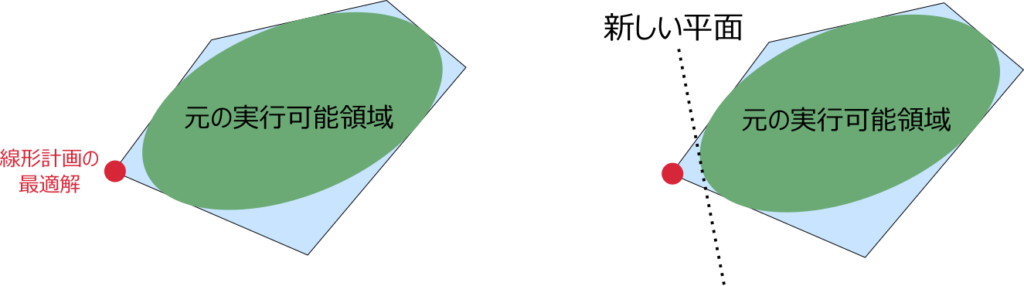
この方法だと、最適値に関係ない領域は細かく近似されることなく自動で放っておかれるので、少ない平面で最適化問題を効率よく近似することができます。
線形計画で最適化できる区分線形関数の例を見てみましょう。
以下の問題は L1 ノルム最小化という信号処理などで登場する問題です。
$$\begin{align}&\underset{x \in \mathbb{R}^{n}}{\text{minimize}} \quad \|x\|_1 \\ &\quad \text{s.t.} \qquad Ax = y\end{align}$$
\(Ax = y\) という成り立ってほしい条件を満たすベクトルのうち、最もノルムが小さい（つまり単純な）ベクトルを探す問題です。ノルムとして L1 ノルムを使うことでスパースなベクトルが解として得られます。
絶対値関数が区分線形であることから分かるように、L1 ノルムは区分線形凸関数です。よって、この問題は区分線形凸関数最小化で解くことができます。
上で議論した内容を踏まえると以下の線形計画と等価です。（記述がシンプルになるように等価な変形を行っています。）
$$\begin{align}&\underset{(x, t) \in \mathbb{R}^{n + n}}{\text{minimize}} \quad \sum_i t_i \\ &\quad \text{s.t.} \qquad Ax = y \\ & \qquad \qquad -x \le t \\ & \qquad \qquad \quad x \le t\end{align}$$
その他の例は線形計画の応用例を参照してください。
- 区分線形凸関数の最小化は線形計画で定式化できる
- 凸関数は区間の数を増やせば区分線形凸関数で近似できる
- L1 ノルム最小化が区分線形凸関数の最小化の例
