線形計画の実行可能領域のさまざまな図形的な特性をみていきます。
最適化問題の決定変数が二次元や三次元の場合は、実行可能領域や目的関数値を図示することができます。
例えば、以下の線形計画問題を考えます。 $$\begin{align*}&\underset{(x_A, x_B) \in \mathbb{R}^2}{\text{maximize}} \quad 80 x_A + 50 x_B \\ &\quad \text{s.t.} \qquad 20 x_A + 30 x_B \le 100 \\ &\qquad \qquad 40 x_A + 20 x_B \le 120 \\ &\qquad \qquad (x_A, x_B) \ge 0\end{align*}$$ この問題の実行可能領域は、\(x_A\) を横軸、\(x_B\) を縦軸に取ると、以下のように図示することができます。
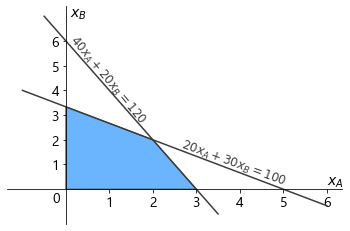
各不等式 \(a_A x_A + a_B x_B \ge b\) は、不等号を等号で置き換えた直線で分割される領域、つまり半平面を表し、全ての制約が成り立つ必要から、実行可能領域はこれらの共通部分となります。
このような理由から、上記の実行可能領域は直線で囲まれた多角形となるのです。
実行可能解の目的関数値を色で表すと以下のようになります。
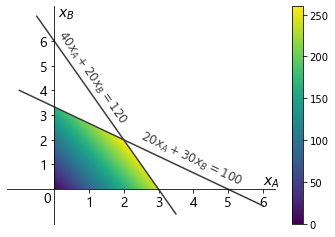
最適化問題は、この領域の中から最も黄色い点を探し出す問題ということになります。この場合であれば、\((x_A, x_B\) = (2, 2)\) が最も黄色い（目的関数値が大きい）ので最適解となります。
三次元の場合であれば、直線が平面に置き換わり、実行可能領域は平面で囲われた領域、つまり多面体となります。
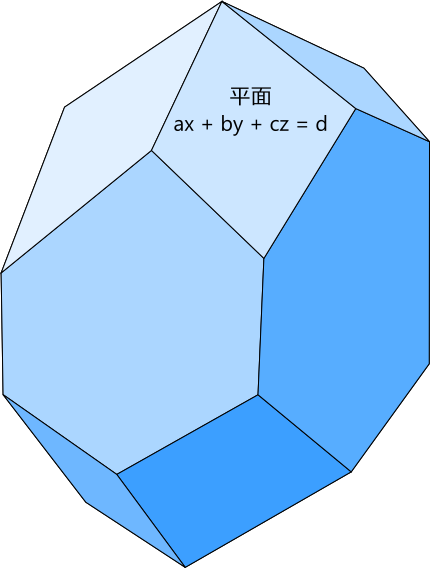
線形計画の実行可能解が凸集合であることを確認します。凸集合の定義は以下のようなものでした。
集合 \(A \subset \mathbb{R}^d\) が凸集合であるとは、任意の \(x, y \in A\) と任意の \(\alpha \in [0, 1]\) に対して、\(\alpha x + (1 – \alpha) y \in A\) となること。
標準形線形計画の実行可能領域 \(\mathcal{C} = \{x \mid Ax = b, x \ge 0\}\) は凸集合である。
\(x, y \in \mathcal{C}, \alpha \in [0, 1]\) を任意に取る。\(z = \alpha x + (1 – \alpha) y\) とおくと、$$Az = \alpha Ax + (1 – \alpha) A y = \alpha b + (1 – \alpha) b = b,$$ $$z = \alpha x + (1 – \alpha) y \ge 0$$ より、\(z \in \mathcal{C}\) となる。よって、\(\mathcal{C}\) は凸集合。
標準形以外の線形計画についても、同様に実行可能領域の凸性を示せます。
線形計画の実行可能領域は凸多面体になります。このことを示したいところですが、そのためには凸多面体の定義を数学的に行わなくてはなりません。一般の次元の多面体の定義の方法は様々ですが、最適化の分野では、「凸多面体とは、行列 \(A\) とベクトル \(b\) を用いて \(\{x \mid Ax \le b\}\) と表せる領域である」と定義されることが多いです。この定義を採用すると、線形計画の実行可能領域が凸多面体であることは定義から明らか、となります。このような理由から、一般の次元において線形計画の実行可能領域が凸多面体であると言うことに情報量は無いのですが、二次元、三次元の場合の類推からイメージがしやすくなることが多いので、線形計画の実行可能領域が凸多面体であると取り立てていうこともしばしばあります。
実行可能領域の基底解が頂点に対応に対応していることを確認します。
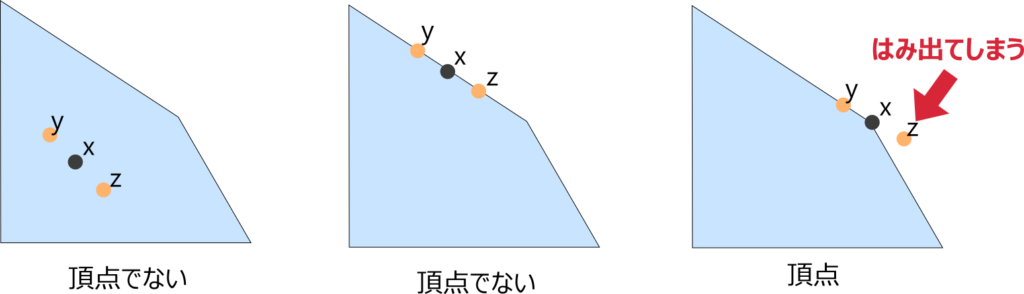
まず、高次元の図形において頂点というものを数学的に定義します。
集合 \(A \subset \mathbb{R}^d\) の点 \(x \in A\) が頂点であるとは、\(\frac{y + z}{2} = x\) となる \(y, z \in A, y \neq x, z \neq x\) が存在しないことである。
つまり、頂点は他の点の中点で表せない点のことです。内点や辺の中点は、両側に \(y, z\) をとれるので頂点ではありません。
次に基底解の定義を復習しましょう。
標準形線形計画問題 $$\begin{align*}&\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad c^\top x \\ &\quad \text{s.t.} \qquad A x = b \\ &\qquad \qquad x \ge 0\end{align*}$$ について、ベクトル \(x \in \mathbb{R}^n\) はある添字集合 \(B \subset \{1, 2, \cdots, n\}\) について以下の 4 つの条件を満たすとき、基底解と呼ばれる。
- \(x\) は実行可能解である (= 制約条件を満たす）
- \(|B| = m\)
- 任意の \(i \not \in B\) について \(x_i = 0\)
- \(A\) のうち、\(B\) に含まれる番号の列を並べた行列 \(A_B\) は正則である
標準形線形計画問題 $$\begin{align*}&\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad c^\top x \\ &\quad \text{s.t.} \qquad A x = b \\ &\qquad \qquad x \ge 0\end{align*}$$ の基底解 \(x\) は実行可能領域 \(\mathcal{C}\) の頂点である
一般性を失うことなく \(B = \{1, 2, \cdots, m\}\) と仮定する。このとき、$$x_{m+1} = \cdots = x_n = 0$$ である。\(\frac{y + z}{2} = x\) となる \(y, z \in \mathcal{C}\) を任意にとる。このとき、\(x\) の値より $$y_{m+1} + z_{m+1} = \cdots = y_{n} + z_{n} = 0$$ かつ実行可能性より $$y_{m+1} \ge 0, z_{m+1} \ge 0, \cdots, y_n \ge 0, z_n \ge 0$$ が成り立つので、$$y_{m+1} = \cdots = y_n = z_{m+1} = \cdots, z_n = 0$$ となる。また、\(x\) のうち、添字 \(B\) に対応する要素を並べたものを \(x_B\) と表すと、等式制約条件より \(A_B x_B = A_B y_B = A_B z_B = b\) となる。\(A_B\) は正則なので \(x_B = y_B = z_B\)。\(B\) 以外の要素がゼロであることと合わせて \(x = y = z\) となる。よって \(x\) は頂点である。
最適解が存在する線形計画問題には基底解の最適解が存在するのでした。この定理より、頂点の最適解が存在するということになります。頂点の最適解が存在することは、冒頭の二次元の図からも想像できるかと思います。
また、シンプレックス法は基底解を順番に探索していくアルゴリズムですが、これは頂点を順番に辿っていくアルゴリズムであると図形的に解釈することもできます。
- 最適化問題を図示することで問題のイメージをつかむことができる
- 線形計画の実行可能領域は凸集合
- 線形計画の基底解は実行可能領域の頂点に対応する
