この章では、半加算器を進化させて全加算器というものを実装します。全加算器は 3 つの二進数 1 桁の足し算を行う回路です。なぜ 3 つの入力を考えるかというと、繰り上げに対処するためです。筆算を考えると分かるように、複数桁の足し算では、下の桁からの繰り上げが発生します。A + B を考えるときも、A の対応する桁 + B の対応する桁 + 繰り上がってきた値でその桁の計算をします。このために 3 つの数の入力が必要となるわけです。
全加算器は 3 つの入力端子 A, B, C をもち、2 つの出力端子 S, D をもつ回路です。直感的には二進数の足し算 A + B + C を表しています。S が一桁目の値、D が繰り上がりです。
全加算器の真理値表は以下のように表されます。
| A | B | C | S | D |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
前章でつくった半加算器を組み合わせて実装します。直感的には、半加算器で A + B を計算したあと、その結果と C の足し算を計算すればよさそうです。どちらかの計算で繰り上がりが発生したときのみ繰り上がりが発生します。なので、全加算器は以下の回路で実装できます。
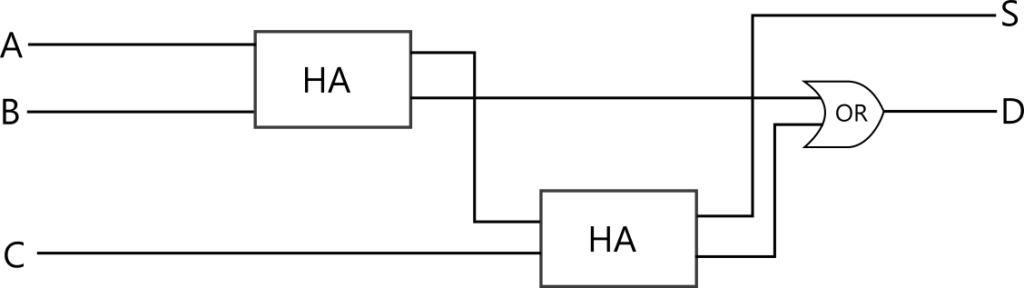
これが全加算器として機能しているかテストしてみましょう。入力が A = 0, B = 1, C = 1 のとき、各点での値は以下のようになり、正しく全加算器の要件が満たされていることが分かります。他の入力でも同様です。
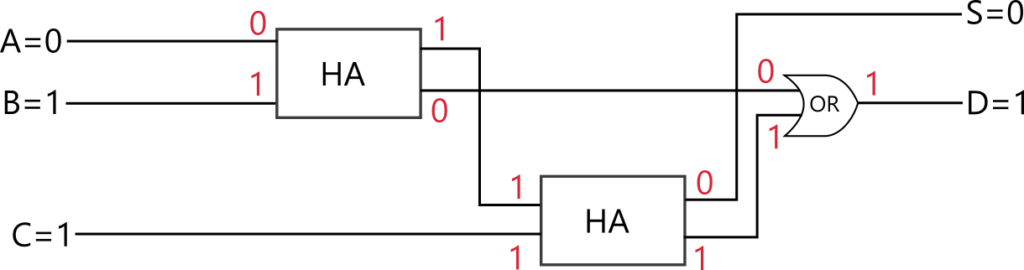
前章で半加算器をつくり抽象化しておいたおかげでかなり簡単に全加算器が実装できました。抽象化の恩恵です。全加算器も抽象化しておきましょう。全加算器 (full adder) は FA と書いた四角で表現することにします。
- 3 つの二進数 1 桁の足し算を行う回路を全加算器という
- 全加算器は繰り上げに対処するのに必要
- 全加算器は半加算器の組み合わせで実装できる
次章ではいよいよ複数桁の足し算を作り、素朴な計算機を完成させます。


