論理回路で最も基本的なパーツを論理素子といいます。ここでは代表的な 3 つの素子を学びます。これらの素子ができる機能は限られていますが、これらを組み合わせてくことで豊富な機能をもった回路を設計することができます。現代のコンピュータもとことんまで分解するとこれらのパーツで表現できるのです。
前章で述べたように、電流が流れている回路を 1、流れていない回路を 0 と表します。例えば、以下のように表すと、A の部分に電流を流し、B の部分に電流を流すと C には電流が流れる。D の部分には電流を流さず、E の部分にも電流さないと F の部分には電流が流れる、ということを表します。線に繋がっている図形が論理素子を表します。
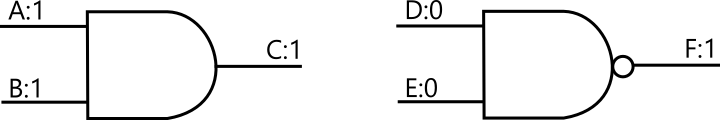
入力で電流を流さないのに出力から電流が流れるというのは変に聞こえるかもしれませんが、論理素子には常に外部から電気が供給されておりそれを使っています。なので、後者の例であれば、入力両方に電流が流れていないことを検知すると、出力ゲートに電流を流す仕組みが素子の中に備わっていると考えてください。
この講義では、これらの素子がどのようにして実現されているかについては踏み込みません。とにかく、このように入力したらこのように出力する素子があると仮定します。実際、そのような仕組みの素子は電気パーツショップに行けば売っています。仕組みについて気になる方は半導体についての教科書を参照してください。
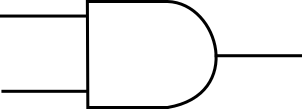
AND 素子は入力端子を二つもち、出力端子を一つもっています。両方の入力が 1 のとき出力は 1 となり、それ以外の場合は出力は 0 となります。その名の通り AND(論理積)演算を表しています。AND 素子は入力側が角張っていて出力側が丸みを帯びた以下のような図で表します。
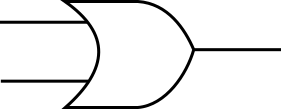
OR 素子は入力端子を二つもち、出力端子を一つもっています。どちらか片方の入力でも 1 のとき出力は 1 となり、両方入力が 0 の場合、出力は 0 となります。その名の通り OR(論理和)演算を表しています。OR 素子は入力側が丸みを帯びてへこんでいて出力側がとがっている以下のような図で表します。
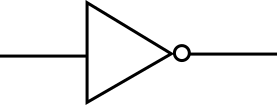
NOT 素子は入力端子を一つもち、出力端子を一つもっています。入力が 1 のとき出力が 0 となり、入力が 0 のとき出力が 1 となります。その名の通り NOT(論理否定)演算を表しています。OR 素子は三角形に小さい丸がついた以下のような図で表します。
- 基本的な論理素子に AND, OR, NOT 素子がある
- これらはそれぞれ論理積、論理和、論理否定演算に対応する
次回からこれらの素子を組み合わせて徐々に複雑な論理回路を構築していきます。


