双対問題: 線形計画入門 8 - コンピュータフリーク

この章では、一般の最適化問題について、双対問題という概念を導入します。双対問題は最適化問題を解析する様々な場面で使われる重要な概念です。この章では、最適化途中の解の良さをはかる指標として双対を導入します。

緩和の考え方

最適化問題 $\begin{align*}&\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad f(x) \\ &\quad \text{s.t.} \qquad h_1(x) = 0 \\ &\qquad \qquad h_2(x) = 0 \\ &\qquad \qquad h_3(x) \le 0\end{align*}$ を考えます。

最適化の途中で実行可能解 $x$ が得られたとします。 $x$ はどのくらい良い解でしょうか？最適でなくても、それなりに良い解なのであれば、ここで探索を打ち切ることで時間の節約になるかもしれません。

例えば輸送コストを最小化する問題だとしましょう。 $f(x) = 220.00$ （万円）だとします。もし最適解 $x^*$ が $f(x^*) = 126.00$ なのであれば、よりよい解を探求することでコストを大幅に改善することができます。一方、 $f(x^*) = 219.98$ なのであれば、これ以上頑張って探索する意味はほとんどないでしょう。

しかし、実際に探索を進めて最適解を見つけるまで $f(x^*)$ の値が分からないことが問題です。

緩和問題というのは、元の問題よりも簡単に解け、元の問題よりも最適解が小さいと分かっている問題です。緩和問題を解くことにより、 $x^*$ を求めるよりも簡単に解の良さを見積もることができます。ここではラグランジュ緩和というものを紹介します

ラグランジュ緩和

上記の最適化問題は、制約条件があることが問題を複雑にしています。そこで、制約条件の無い緩和問題を考えます。

単に制約条件を消して、 $\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad f(x)$ とするだけでも緩和問題にはなっているのですが、この問題の最適値はもとの問題よりも低くなりすぎ指標として役に立ちません。簡単に解ける範囲で、できるだけ元の問題に近いような緩和問題を考えることが重要です。

準備として、 $\mathcal{I}_{0}(x) = \begin{cases} 0 & (x = 0) \\ \infty & (x \neq 0)\end{cases}$ $\mathcal{I}_{-}(x) = \begin{cases} 0 & (x \le 0) \\ \infty & (x > 0)\end{cases}$ という関数を考えます。例えば $\mathcal{I}_0(h(x))$ は制約 $h(x) = 0$ を満たすのであればゼロ、制約違反では $\infty$ を示します。

これらの関数を使うと、もとの最適化問題は $\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad f(x) + \mathcal{I}_{0}(h_1(x)) + \mathcal{I}_{0}(h_2(x)) + \mathcal{I}_{-}(h_3(x))$ という等価な問題に変換できます。元の問題で実行可能でない解に対しては 2, 3, 4 項目のいずれかが $\infty$ になるので最適解にはなりえず、実行可能解の中で $f_(x)$ が最小なものがこの問題の最適解になります。この問題は緩和ではなく、完全に等価な問題であることに注意をしてください。この問題は表面上は制約の無い問題ではあるのですが、目的関数の値を計算するのに場合分けが入るので、書き方を改めただけの実質的には制約条件つきの問題になっています。

この目的関数から場合分けのない下界を構成します。

$\mathcal{I}_{0}(h(x))$ について

補題

任意の実数 $\lambda \in \mathbb{R}$ について、 $\lambda h(x) \le \mathcal{I}_{0}(h(x))$ が成り立つ

これは、 $h(x) = 0$ のとき両辺ゼロ、それ以外のときは右辺が $\infty$ となるので明らかです。グラフで表すと以下のようになります。

$\mathcal{I}_{-}(h(x))$ について

補題

任意の非負実数 $\lambda \ge 0$ について、 $\lambda h(x) \le \mathcal{I}_{-}(h(x))$ が成り立つ

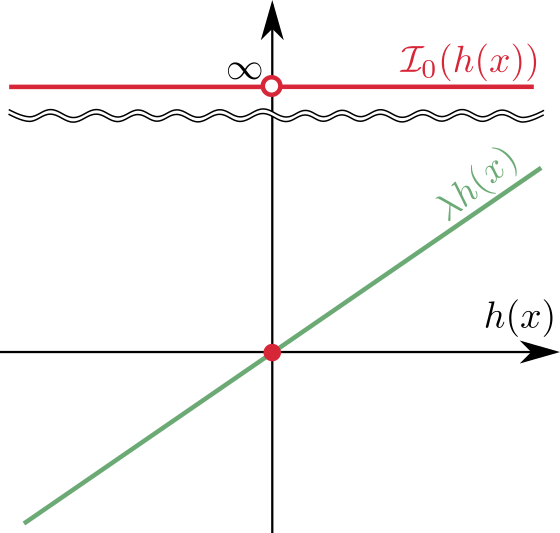
これは $h(x) \le 0$ のとき左辺は非正で右辺がゼロ、 $h(x) > 0$ のとき右辺が $\infty$ になるので明らかです。グラフで表すと以下のようになります。

ラグランジュ緩和問題

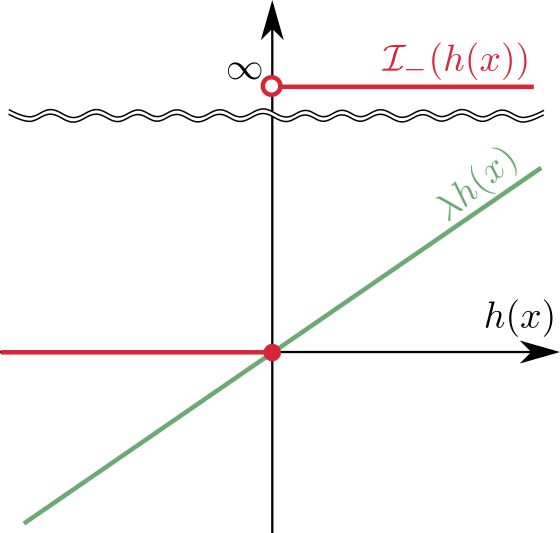
一般に、最適化問題 $\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad f(x) + \sum_{i = 1}^m \mathcal{I}_{0}(h_i(x)) + \sum_{i = m + 1}^p \mathcal{I}_{-}(h_i(x))$ を考えます。

適当な実数 $\lambda_1, \cdots, \lambda_m \in \mathbb{R}$ および非負実数 $\lambda_{m+1} \cdots, \lambda_{p} \ge 0$ について $\underset{x \in \mathbb{R}^n}{\text{minimize}} \quad f(x) + \sum_{i = 1}^m \lambda_i h_i(x) + \sum_{i = m + 1}^p \lambda_i h_i(x)$ をラグランジュ緩和問題といいます。各 $\lambda$ についてのこの問題の最適値を表す関数 $g(\lambda) = \min \left(f(x) + \sum_{i = 1}^m \lambda_i h_i(x) + \sum_{i = m + 1}^p \lambda_i h_i(x)\right)$ をラグランジュ双対関数といいます。

上述の補題より、

系

任意の実数 $\lambda_1, \cdots, \lambda_m \in \mathbb{R}$ および非負実数 $\lambda_{m+1} \cdots, \lambda_{p} \ge 0$ について、 $f(x) + \sum_{i = 1}^m \lambda_i h_i(x) + \sum_{i = m + 1}^p \lambda_i h_i(x) \le f(x) + \sum_{i = 1}^m \mathcal{I}_{0}(h_i(x)) + \sum_{i = m + 1}^p \mathcal{I}_{-}(h_i(x))$ が成り立つ

よって、ラグランジュ緩和問題は実際に緩和問題になっています。これを弱双対定理といいます。

弱双対定理

任意の実数 $\lambda_1, \cdots, \lambda_m \in \mathbb{R}$ および非負実数 $\lambda_{m+1} \cdots, \lambda_{p} \ge 0$ について、ラグランジュ双対問題の最適値は、もとの最適化問題の最適値の下界になっている。つまり、もとの最適化問題の任意の実行可能解 $x$ に対して、 $g(\lambda) \le f(x)$ が成り立つ

証明

任意の実行可能解 $x$ に対して、実行可能性より $\mathcal{I}_{0}(h_i(x)) = 0$ が成り立つので、 $\begin{align*}f(x) &= f(x) + \sum_{i = 1}^m \lambda_i h_i(x) + \sum_{i = m + 1}^p \lambda_i h_i(x) \\ &\ge f(y^*) + \sum_{i = 1}^m \lambda_i h_i(y^*) + \sum_{i = m + 1}^p \lambda_i h_i(y^*) \\ &= g(\lambda)\end{align*}$ が成り立つ。ここで $y^*$ はラグランジュ双対問題の最適解。 $x$ としてもとの最適化問題の最適解を取ると、ラグランジュ双対問題の最適値が下界になっていることが分かる。

つまり、適当に $\lambda$ を定めてやり、ラグランジュ双対問題を解くことでもとの問題の解の良さを見積もることができます。ラグランジュ双対問題は制約条件がないので、比較的簡単に解くことができます。

たとえば、冒頭の例のように、 $f(x) = 220.00$ という実行可能解 $x$ が見つかっているとき、適当な $\lambda$ に対してラグランジュ双対問題の最適値が $219.96$ だったとすると、もとの最適化問題の値はこれより下げられないことが分かるので、これ以上頑張って探索する意味はないと結論づけることができます。

ただし、 $g(\lambda)$ は最適値以下であることが保証されているだけで、どれだけ最適値に近いかは保証されていません。たまたま $f(x)$ に近い値が出てくれれば、これ以上頑張って探索する意味はないと結論づけることができますが、たとえ $f(x)$ が最適値に近くても、 $g(\lambda)$ は非常に低い値を出してしまい有益な結論が引き出せない場合もあります。

そこで、できるだけよい $\lambda$ を見つけようというのが自然です。その問題を双対問題といいます。

定義: 双対問題

$\begin{align*}&\underset{\lambda \in \mathbb{R}^{p}}{\text{maximize}} \quad g(\lambda) \\ &\quad \text{s.t.} \qquad \lambda_i \ge 0 \quad (i = m+1, \cdots, p)\end{align*}$ を双対問題という

もとの問題が最小化問題だったのに対して、双対問題は最大化問題であることに注意してください。任意の実行可能な $\lambda$ に対して $g(\lambda) \le f(x^*)$ なので、双対問題の最適値はやはり $f(x^*)$ の下界になっています。ただし、あらゆるラグランジュ双対問題の中で、もっとも大きい下界です。

双対問題は一般に簡単に解けるとは限りませんが、線形計画問題に関していえば、双対問題も線形計画問題になり、しかもその最適値は $f(x^*)$ にちょうど一致するというよい性質を持っています。線形計画の双対については次の章で議論します。